[Python源码剖析] Python对象初探
在Python的世界里,一切都是对象。面向对象概念中的实例是对象,类也是对象。特别地,像Python中的int,string,dict等则称为内建类型对象。当然,我们也可以自定义对象。
Python中的对象在C级别就是一块内存而已,而且通常不能被静态初始化,也不能在栈上生存,唯一的例外就是类型对象。而当一个对象被创建之后,它在内存中的大小就不变了,所以像list等可变长的对象都需要在其内部包含一个指针变量。
所有对象的基石是PyObject结构体,而其中主要就是宏PyObject_HEAD,里面主要是两个字段
int ob_refcnt; // 引用记数 struct _typeobject *ob_type; // 类型对象的指针
实际上,所有的对象的内存排布上都必须以PyObject_HEAD开头,然后才是具体类型相关的变量(或者说是扩展),比如PyIntObject的扩展变量是long ob_ival。这样的目的就是用一个PyObject*指针就可以引用任意一个对象。
对应于变长对象,还有一个PyVarObject结构体,其主要的内容是宏PyObject_VAR_HEAD开头,其相对于PyObject_HEAD就是多出一个变量int ob_size,即变长对象中的item数量。
后面来说类型对象,正如前面所述,它就是面向对象概念中的“类”。类型对象以PyTypeObject结构体来定义,它以PyObject_VAR_HEAD开头,后面包括类型的名称,与分配空间大小有关的变量,该类型可以支持的各种函数集合的指针等。具体的一个类型,比如PyInt_Type就是PyTypeObject结构体的一个实例而已。
对象的创建有两种途径:范型API,称为AOL;与类型相关的API,称为COL。不多说了。
PyIntObject被创建的过程:实际上Python中的int对应于PyInt_Type,而其父类object的类型对象则是PyBaseObject_Type。首先,PyInt_Type中的tp_new会被调用,如果为空的话,会向上找其父类,即PyBaseObject_Type的tp_new来申请内存,申请过程会用到PyInt_Type中的tp_basicsize等信息。申请内存完成后,继而会调用PyInt_Type中的tp_init来做初始化。对应到C++中,tp_new就是new操作符,而tp_init则可视为构造函数。
对象被创建后,其行为其实大多是由其类型对象中所定义的各种函数集决定的,例如,在PyTypeObject中有tp_as_number, tp_as_sequence, tp_as_mapping三个函数族,分别对应于对象被用作数字,序列和映射时该如何表现。例如,重写一个__getitem__函数实际就相当于指定了PyTypeObject中tp_as_mapping.mp_subscript操作。
一个有趣的现象是PyTypeObject也是以PyObject_VAR_HEAD开头的,所以它也需要指定一个类型对象作为它的对象,亦即“类型的类型”,这就是PyType_Type,它也被称为metaclass。
Python对象的多态性是通过其类型对象指针ob_type动态决定的,例如object->ob_type->tp_print(object)。
PyObject中的都会一个引用计数,即ob_refcnt变量。C源码中主要是通过Py_INCREF和Py_DECREF两个宏来增加和减少一个对象的引用计数的。当引用计数变为0时,Py_DECRF会调用该对象的析构函数来尝试释放其占有的内存(tp_dealloc)。当然,类型对象是超越引用计数规则的,它永远不会被析构。而即使一个对象调用了析构函数,也不一定会释放内存,因为Python大量使用了内存对象池技术,避免反复对OS申请内存而造成性能问题。
[PGM] Section 4. Representation-Local Structure
Overview
对于一个条件概率分布\(P(Y|X_1,...,X_N)\),如果假设每个变量都可以取K个值,那么完全使用表格的形式(tabulor representation)来描述这个分布的话,需要有\(K^(N+1)\)行,即指数级。
幸运的是,变量之间往往存在一些其它的局部结构关系(local structure),使得我们不需要这么行就能描述,甚至很compact地描述出这个条件分布。例如,Deterministic CPD, Tree-structured CPD, Logistic CPD, Noisy OR, Linear Guassian,本section后半部会都会涉及到。
先给出几个概念
- General CPD: 任何一个满足归一化条件的函数\(\phi(X,Y_1,...,Y_k)\),都可以称为一个General CPD,即对所有的\(y_1,...,y_k\),\(\sum_x \phi(x,y_1,...,y_k)=1\)。
- 特定上下文独立(Context-Specific Indepedence):\(P \models X \perp_c Y | Z, c\),c可以是一些其它变量的具体取值。
Tree-Structured CPD
如下图所示,这是实际是\(P(J|L_1,L_2,C)\)的条件概率分布,如果没有局部结构的话,那么应该有\(2^3=8\)个概率分布,而图中只有4个概率分布产出,这就是局部结构将问题简化了。
Choice可以看作学生寄出了第一种推荐信还是第二种,Job表示工作申请是否被接收。这里实际上存在着一个上小节中的概念“Content-Specific Independence”,具体来说,就是\(P \models (L_1 \perp_c L_2 | J, c)\),例如学生只寄出了第一种推荐信,并且最后申请未成功,那么公司是否接收到了那封信的概率不会被公司是否接收到了第二种推荐信影响(因为第二封绝对没有寄出,公司以概率100%未收到这封信)。
这个Choice也称为Mulitplexer,它唯一地选择了一条路径。更一般地,
其中变量A就是multiplexer,是一个离散值,它的取值范围是1...K,而Y的取值以概率1等于\(Z_A\)。
Independence of Causal Influence
Noisy OR CPD
举例来说,引起咳嗽的原因可能有很多,可能是流感,普通感冒,过敏,甚至是偶然,这些原因对产生咳嗽这个结果是OR的关系。
图中每个\(Z_i\)表示\(X_i=1\)被触发的情况下,它本身是否成功产生了咳嗽。其可能性为\(P(Z_i=1|X_i)=\lambda_i\)。给定这个结构,那么最终产生咳嗽的可能性需要考虑所有这K个可能的因素,得到\(P(Y=1|X_1,...,X_k)\),计算方式如上图所示。
除了Noisy OR之外,还可以有Noisy AND/MAX等,只是计算\(P(Y=1)\)的方式不同。
Sigmoid CPD
由于sigmoid函数本身的值域就是0-1之间,所以其输出可以看作是一个概率值(实际是CRF,后面的章节有提到)。其它的地方也没啥新鲜的,只是通过线性模型从各个\(Z_i\)得到\(Z\),再输入到sigmoid函数里。当权重\(w\)的尺度被放大后,斜率变大,sigmoid的函数图像就会更sharp一些。
Continuous Variables
前面的Y都是离散变量(实际上都是0-1变量),下面的是连续型变量,像下面这个例子中,目标变量是S(传感器对温度的度量值),这是一个正态分布的连续变量,它在下一时刻结果依赖于外界温度O和室内温度T两个方面,并利用线性插值得到正态分布的期望值(线性高斯模型Linear Gaussian)。如果也考虑到是否开着门这个离散变量D,那么不同条件下正态分布的参数(插值参数,方差)是不同的,这样就变成了Conditional Linear Gaussian。
不废话了,直接上图
有线性高斯,也就必然可以有非线性的。课程中给了几个例子都没太懂,只是知道有这个么个非线性的东西应该就成了。
[PGM] Section 3. Representation-Template Models
Overview
模板模型实际就是在变量的基础上做了一层抽象,其中的一个模板变量可以实例化成N个实际的变量。
以血型为例,A的血型依赖于A的父母,而B的血型也依赖于B的父母,等等。而子女与父母之间的这种依赖关系以及之间参数(具体来说就是CPD)则是通用的,是可以在两个家族间共享的。同样的,A的后代的血型同样也是依赖于A及其配偶的血型,因此这种参数甚至还可以在同一个家族内共享。
类似的例子还有前面那个学生S,课程C和得分G的例子,不同的学生在不同的课程有不同的得分,但是他们之间共享S,C,G之间结构及其CPD参数。
模板变量:一个模板变量\(X(U_1, U_2, ..., U_k)\)可以实例化多次,即\(U_i = u_i\),如果血型的例子,则模板是Genotype(person),实例化后的变量则是Genotype(A), Geontype(B), ......
模板模型:这个东西就是描述实际变量如何从模型中继承依赖关系的一种语言。下面介绍的Dynamic Bayesian Networks就是描述时序模型的一个模板。
时序模型 Temporal Model
以X(t)表示随机变量X在时刻t的取值,对任意的t<=t',X(t:t')表示X(t)至X(t')的若干个变量,时序模板的目的就是要表示这一系列变量的联合概率分布P(X(t:t'))。
两个基本假设
- Markov Assumption: X(t)的取值依赖于之间一个时刻的X(t-1)的取值,而与其它时刻无关(独立);
- Time Invariance: 时间不变性,即\(X(t+1|t) = X(t+k+1|t+k) = X(t'|t)\)。
前面的两个假设不一定在所有场景下都是适用的,因此可以再扩展一下,X可以不止是一个随机变量,而是一个状态(state),而这个状态可以是若干个随机变量组成。例如,一个机器人在某时刻的位置为Loc(t),那么其下一个时刻的位置并不只依赖于这个Loc(t),还与当前进的方向,前进的速度等参数有关,因此可以抽象一下,以State(t)作为一个单位,表达这个时刻下各个因素的联合分布,而其下一个状态State(t+1)则完成依赖于这个State(t)。总结来说,就是redesign the model。
有了这两个简化的假设之后,后面就好办了,因为我们只需要给出一个初始状态,再给出一个从t到t+1的转移模型,这事儿就搞定了。
-
初始状态比较容易描述,实际就是把初始状态下各个变量之间的关系及具体的CPD参数用BN(0)表达。
-
转移模型可以使用2-time-slice Bayesian Network(2TBN)来描述。
2-time-slice Bayesian Network(2TBN)
定义于变量\(X_1, ..., X_N\)的转移模型2TBN是一个BN的片段,其中的结点包括\({X'}_1,...,{X'}_N\)以及\(X_1, ..., X_N\)的一个子集,且仅有前者有对应的父结点及CPD。它们联合表达了以下条件分布
\[P(X'|X) = \prod_i P({X'}_i|Parent({X'}_i))\]
带有初始状态的2TBN称为一个DBN。
Ground Network(Dynamic Bayesian Network)
对于一个时间序列0...T, 其对应的Ground Network的结构为
- \(X_1^{0},...X_n^{0}\)的模型为BN(0)
- \(X_1^{t},...X_n^{t}\)的模型为DBN
隐马尔科夫模型HMM
课程这里只简单介绍了下,没有深入细节,主要篇幅花在了语音识别的应用上。
HMM可以看作是BN的一个子类,但是它的变量之间的级别上几乎就没有复杂的结构关系,它主要的特点是在转移矩阵上的稀疏性和重复性,即它的复杂性体现在同一个变量在不同时刻取值的变化的转移概率分布。
HMM的主要应用领域包括语音识别,自然语言处理等。
模板模型Plate Model
正如overview里所述,模板模型的核心就是share across and within diferrent models。比如翻硬币的例子,每次的结果都是一个iid的随机变量,而它们的取值(正,反)分布是相同的。下图中,每一个outcome被使用t作为index表达是哪一次的toss的结果。
再复杂一点的模板,例如Nested Plates & Overlapped Plates,直接上图。
每个D使用c作为index,即每个课程有一个难度值,而I和G使用(c,s)作为index,也就是说每个学生上每门课都会有个分数,而每个学生上每门课时都有一个适合度(在这方面是否够聪明)。
如果认为学生的聪明程度不依赖于一门课程的话,那么上面的这个模型就不合适了,于是就有了Overlapped Plates
同一个模板下衍生出来的模型都是共享参数据,像这里的\(P(G|D,I)\)等等。后面还提了一个Collective Inference,就是用若干个衍生出的了模型来做全局的推演,没太懂,就不费话了。
最后正式给出Plate Dependency Model的定义
对于一个模板变量\(A(U_1, ..., U_K)\),其中\(U_i\)为index,它们若干个模板父变量\(B_1(PU_1),...,B_m(PU_m)\),其中每个\(PU_j\)都是\((U_1, ..., U_K)\)的一个子集(No indices in parent that are not in child),那么就可以定与其相关的一个CPD \(P(A|B_1,...,B_m)\)。
当把模板变量实例化为\((u_1, ..., u_K)\)之后,它就形成一个实例的网络。
关于前面的那个子集的约束,举例来说,假如G(c, s)表示一个学生在某门课上的得分,那么它不能作为这个学生整个评价的父结点(整体评价只与s相关,即Eval(s)),这需要集合所有c的G(c, s)才能形成一个有实际意义的CPD。
安装Hadoop
第一次尝试在自己的笔记本上安装单机的Hadoop,啥也不懂,上网瞎搜,找到个“超详细”版的文章,相当给力。
我之前安装过OpenJDK,所以跳过了安装SUN-JDK这一步,而$JAVA_HOME的位置也有所不同,我的位置在
/usr/lib/jvm/java-1.7.0-openjdk-i386
Hadoop的版本我下载的是1.1.2,要下载stable版本的,不然话找不到配置文件位置。
hadoop-1.1.2.tar.gz
其它的都大同小异,配置和启动过程都差不多。
对为啥要安装ssh服务不太理解,网上搜了下,貌似是因为namenode管理各个datanode的启动和停止都是通过无密码验证的ssh来进行的,参考内容在这里。
以后可以抽空在hadoop上玩玩儿了。。。
[PGM] Section 2. Representation-Bayesian Networks
Semantics and Factorization
直接上一个文中给出的例子,随机变量是课程难度D,学习智力I,课程成绩G,推荐信L,学生的SAT分数S(不知道具体是啥东西)。每个随机变量对应图中的一个结点。
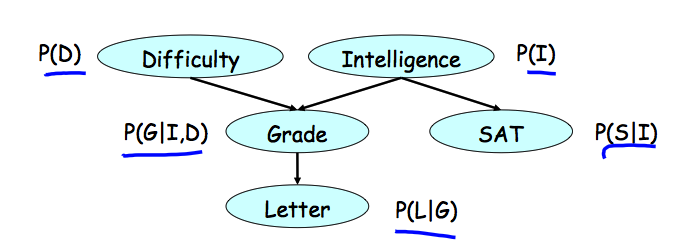
各个变量之间的依赖关系则由图中的箭头表示,每个结点与其所有父结点共同形成一个局部的条件概率分布,例如G的取值条件依赖于D和I的取值,而没有父结点的变量则只有一个边缘分布或者先验分布。
图中的结点和结点间的关系有效地表示了条件概率分布,而各变量的联合分布则可以通过这些条件概率分布(或者更一般地,因子)之间的乘积来表达。实际上,每个联合分布都可以写成chain rule的形式,而利用图中表达出的条件独立性进行简化,得到的就是各个条件概率分布的乘积。建议自己动手搞一下,更容易理解。
下面给出几个相关的定义
- Bayesian网络定义为一个有向无环图(DAG)G,每个结点表示一个随机变量\(X_1, ..., X_n\)。对于每个结点\(X_i\)都有一个对应的CPD(条件概率分布),表示为\(P(X_i|Par_G(X_i))\)。
- Bayesian网络通过链式规则表达一个联合概率分布\[ P(X_1, ..., X_n) = \Pi_i P(X_i|Par_G(X_i))\]
- 令G为一个关于\(X_1, ..., X_n\)的Bayesian网络,那么如果其联合概率分布P可以表达为上面的链式形式,那么就说P factorizes over G。(不知道怎么翻译,直接copy了)
Reasoning Patterns
- Causal Reasoning:由因及果(这里的因果用得都不准确,只是为了便于理解),例如,学生智力I越高,其得到推荐信L的概率越高,即\(P(l^1) < P(l^1|i^1)\)。顺向箭头的方向的影响。
- Evidential Reasoning:由果推因,例如,观察到学生的课程得分很低时,那么这门课难度高的可能性更大,即\( P(d^1) < P(d^1|g^3)\)。逆着箭头方向的影响。
- Intercausal Reasoning: 两个因之间的影响,例如,观察到得分很低时,学生智力可能较低,但如果同时观察到课程很难时,那么学生智力可能未必有那么低,即\( P(i^1|g^3) < P(i^1|g^3, d^1)\),如果再已经学生的SAT很高,那么课程难度可能就更高。再例,Z = X | Y,给定Z=1时,X和Y为1的概率都是2/3,但是如果给定了Y=1(Y explains away Z),那么X=1的概率就降为了1/2。
Flow of Probabilistic Influence
啥时候X可以影响到Y
| 方向 | 是否可以影响到 |
| X->Y | YES |
| X<-Y | YES |
| X->W->Y | YES |
| X<-W<-Y | YES |
| X<-W->Y | YES |
| X->W<-Y | NO |
简单来说,XY有因果关系时,或者同为果时可以影响到,而同为因时无法影响到。需要注意的是,这里的同为因的情况与前面Intercausal Reasoning中的例子不同,这里没有给定果W的取值。鉴于最后一种情况的特殊性,把X->W<-Y称为V结构(v-structure)。
活跃路径(Active Trails):一条路径\(X_1-X_2-...-X_n\)是活跃的,如果整条路径中不存在V结构,即\(X_(i-1) -> X_i <- X_(i+1)\)。
啥时候在给定Z的情况下X能影响到Y
| 方向 | W not in Z | W in Z |
| X->W->Y | YES | NO |
| X<-W<-Y | YES | NO |
| X<-W->Y | YES | NO |
| X->W<-Y | NO | YES |
这里面的最后一行可以跟上小节里的例子对应上了。
用最开始那个图给出一个例子,S-I-G-D这条路径,啥时候S能影响到Y?当给定Z时,或者啥都没给定时,S无法影响到D,而未给定I并且给定G的情况下时,S可以影响到D。
活跃路径(Active Trails):给定Z的情况下,一条路径\(X_1-X_2-...-X_n\)是活跃的,如果其满足以下两个条件
- 对于任何一个V结构\(X_(i-1) -> X_i <- X_(i+1)\),有\(X_i\)或者至少一个其后续存在于Z之中;
- 没有其它的变量位于Z之中。
Independencies
对于随机变量X和Y,定义独立性\(P \models X \perp Y\),如果满足
- \(P(X, Y) = P(X)P(Y)\)
- \(P(X|Y) = P(X) \)
- \(P(Y|X) = P(Y) \)
条件独立性,跟前面条件一样,只是每个term后面加了个|Z。不再详述了。
举个例子,硬币作为一个变量C,每次投出的结果作为变量\(X_i\),那么可知\(P \models X_1 \perp X_2\)不满足,但是\(P \models X_1 \perp X_2 | C\)。
条件性可能使用变量中的独立性失去,例如前面的例子,给定一个果后,两个因就不再相互独立了。
Bayesian Networks
d分离:如果在给定Z的条件下,G中不存在一条X-Y之间的活跃路径,那么就说X与Y是d分离的(d-spearated),记为\(d-sep_G(X, Y|Z)\)。
注意,d分离只是面向G的定义,与某个P没有直接关联。下面这个定理做了这件事:
定理:如果P factorize over G,并且满足\(d-sep_G(X, Y|Z)\),那么P满足\(X \perp Y | Z\)。证明过程使用了对不同变量分离\(\Sigma\)的方法,具体过程略。
换句话说,如果factorize成立,那么从G中读出的每一个d分离,P中都有一个条件独立性与之对应。例如,G中任一结点在给定父结点后,都与其子结点d分离,于是通过定理可知,如果factorize成立,那么P中任意一个变量都在给定父变量后,与其子变量相互独立。
收集所有G中的d分离,并通过定理可知:“G中所有的d分离的集合”必有一个“条件独立性集合”与之对应,这个由G引出的条件独立性集合定义为 \(I(G) = \{(X \perp Y| Z): d-sep_G(X \perp Y|Z)\}\)。注意,I(G)是G的函数,它只是定义一个条件独立性的集合,对于任意一个给定的P,它可能满足I(G),也可能不满足。而当P满足I(G)时,我们就说G是P的一个I-map。一个特殊的情况,I(G)为空集时,它是所有P的I-map。
Factorization => Indepenence
- 如果P factorize over G,那么G是P的一个I-map;
- 如果G是P的一个I-map,那么P factorize over G
需要注意的是,一般情况下,G中表现出的独立性未必是P中包括的所有的独立性,很可能只是一个子集,但是只要P能够满足I(G),那么G就是P的I-map,P就可以factorize over G,完全encode P中所有独立性的图并不是G。
至此,P与G之间关于独立性的关联已经建立起来。最后抄一段PPT中的总结:

Naive Bayes
朴素贝叶斯假设\(X_i \perp X_j | C\) for all \(X_i, X_j\),即在图模型的表示中每个\(X_i\)只与类变量\(C\)相关联,与不同\(X_i, X_j\)无关联。基于这个假设,可得联合概率分布为
\[P(C, X_1, ..., X_n) = P(C)\Pi_{i=1}^{n}P(X_i|C)\]
朴素贝叶斯分类器(假设只有两类),实际就是比较两个类的后验。
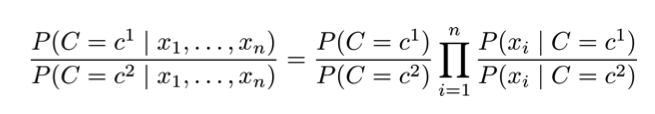
朴素贝叶斯分类器应用于文本数据
- Bernoulli朴素贝叶斯:每个\(X_i\)表示一个字典中的term,\(P(X_i = 1|C)\)表示这个term出现在这个类C中的可能性,归一化条件为\(P(X_i = 1|C) + P(X_i = 0| C) = 1\)。
- Multinomial朴素贝叶斯:每个\(X_i\)表示一个实际出现在文档中的一个位置,\(P(X_i = "cat"|C)\)表示该位置出现的词为cat的可能性,归一化条件为\(\sum_{i=1}^{n}P(X_i|C) = 1\),其中n为字典中词的个数。
朴素贝叶斯的优点是容易搞,容易算,feature间弱相关时很给力,但是当feature间有强相关时,表现得就不咋地了。
[PGM] Section 1. Introduction
注:Coursera的PGM是我在2012后半年跟的网上课程,当时课时很赶,天天在赶作业,没有做太详细的总结,学完之后觉得还是挺有信息量的,所以打算现在再复习一遍,顺便把知识总结一下。
Motivation and Overview
概率图模型英文全称为Probabilistic Graphical Model,先解释一下各自的含义,概念比较虚可以结合后面的具体内容来理解。
- Model: 即Declarative Representation,或者说一个框架结构。这个结构可从给定的训练数据中学习得到或者通过专家设计。框架中一般有若干个参数,使用不同的算法来做训练training(with and without complete data)可以得到模型参数的取值,而在此之后就可以用这个带有参数的模型做对其它样本点来做推演inference(可以是exact,也可以是approximate)。
- Probablistic:用于表示数据中的不确定性,例如不完整的样本,噪声以及无法被Model识别出来的知识等。概率论提供了表达不确定性的工具,例如多元变量的联合概率分布等。
- Graphical: 利用图像的形式表达随机变量之间的依赖关系,例如贝叶斯网络(有向图)或者马尔科夫网络(无向图),temporal,plate models。变量之间的这种依赖关系也可以看作一种约赖,从而可以大大降低Model中独立参数的数量。
Preliminaries: Distributions
一些简单的概念
- 联合概率分布:最简单地可以表示成表格的形式;多个变量之间可能存在的独立性
- 条件概率分布:对联合概率分布表格的reduction and normalization
- 边缘概率分布:通过求和消除掉某些随机变量
Preliminaries: Factors
因子\( \phi(X_1, ..., X_k) \)定义为一个函数 \( Val(X_1, X_k) -> R\),而这个因子的域scope为\( \{X_1, ..., X_k\} \)。
概率分布都可以看作是特殊的因子,而因子概念本身则更加一般,因为它不需要遵守sum-to-one规则。因子可以看作是构建和操控概率分布的基础。
因子的操作
- Factor Product: \( \phi(A,B,C) = \phi_1(A,B)*\phi_2(B,C) \)
- Factor Marginalization: \( \sum_C \phi(A,B,C) \)
- Factor Reduction: eliminate some table rows, leave the rest (unnormalized)
PRML Notes - 3.4 Bayesian Model Comparison
贝叶斯方法避免过拟合是通过边缘化模型参数而实现的,而不是像极大似然那样来做点估计。这样,不同的模型可以使用全部数据来做训练,并进行比较,而不是像CV那样需要拆出一部分来做检验。
假设我们有L个模型,\(M_i, i = 1...L \)。训练数据是从其中一个模型中生成的,即其中有一个是真实模型,但是我们并不确定是哪一个。这种先验的不确定性可以通过先验的均匀分布来表达,而相应的后验分布则表达了我们在观测到数据后,对各个模型的偏好程度。
\[ p(M_i|D) \propto p(M_i) p(D|M_i) \]
由于前面使用的均匀分布做为先验,区分度主要落在了model evidence上面,即\( p(M_i|D) \),它表达了训练数据对各个模型的偏好程度。这个值也称为边缘似然性,因为它是对整个模型的似然性(不是针对某一个参数值)。两个模型的model evidence的比例称为贝叶斯因子。
\[ Bayes Factor = \frac{p(D|M_i)}{p(D|M_j)} \]
一旦我们得到的对各个模型的后验分布,我们就可以使用它来形成一个混合的预测分布,各个模型以后验概率做为权重对其输出的响应值进行加权。一种简化的方式是使用后验最高的模型来做预测,这个选择的过程就称为模型选择。
对于一个参数模型,model evidence的表达式为
\[ p(D|M_i) = \int p(D|w, M_i) p(w|M_i) dw \]
做一些近似的考虑,假设参数的后验分布尖锐的分布在最大值\(w_{MAP}\)周围,宽度为\(\delta w_{posterior}\),并假设参数的先验为\( p(w) = 1/\delta w_{prior}\),那么model evidence可以写成
\[ p(D) = \int p(D|w) p(w) dw = p(D|w_{MAP}) \frac{\delta w_{posterior}}{\delta w_{prior}} \]
对应地,其对数似然性为
\[ lnp(D) = lnp(D|w_{MAP}) + \frac{\delta w_{posterior}}{\delta w_{prior}} \]
由上式可知,当似然性越高时,evidence值越大,然而当参数值极好地拟合训练数据时,evidence越小,即模型复杂度越高,evidence越小。最优的模型应该是在两都之间取一个折中。
从模型生成数据集的角度来看,实际上,过于简单的模型灵活性不够,只能以较低的可能性生成给定的训练数据,而过于复杂的模型则灵活性过大,可能产生的数据集种类更多,产生给于训练数据的可能性也变低(概率被平分)。
对于一个特定的数据集,有可能存在非真实模型的model evidence高于真实模型,而期望意义上这是不可能存在的。假设有两个模型,其中\(M_1\)为真实模型,那么二者在所有数据集上的平均贝叶斯因子表达式为
\[\int p(D|M_1) ln \frac{p(D|M_1)}{p(D|M_2)} dD \]
这个统计量称为KL距离,当且仅当两个分布相同是取零,其它情况下均大于0,因此平均意义下贝叶斯因子是偏向于选择真实模型的。
与其它方法一样,贝叶斯模型选择是对模型的形式有所假设的。例如,当先验分布是improper的时候,model evidence不是良定义的。但是先得到两个模型的贝叶斯因子的表达式,再取极限仍然有可能得到一些有用的结论。
虽然贝叶斯模型比较方法可以省去CV的过程,但是保留一份独立的测试数据来做最终系统的效果评估仍然是明智之举。
PRML Notes - 3.3 Bayesian Linear Regression
贝叶斯框架下的线性回归解决了频率框架下出现的过拟合问题,它是通过在推演阶段对参数引入先验分布,以及在决策阶段对参数值做积分来实现的。
参数分布
假设噪声精度\( \beta \)是已知的,那么似然性函数\( p(t|\mathbf{w}) \)就是一个未知参数\( \mathbf{w} \)的二次函数的幂。根据第二章的内容,其对应的共轭先验分布为正态分布
\[ p(\mathbf{w}) = N(\mathbf{w} | m_0, S_0) \]
而其后验分布同样也是正态分布
\[ p(\mathbf{w}|\mathbf{t}) = N(\mathbf{w} | m_N, S_n) \]
\[ m_N = S_N (S_0^{-1} m_0 + \beta \Phi^{T} \mathbf{t}) \]
\[ S_N^{-1} = S_0^{-1} + \beta \Phi^{T} \Phi \]
最 大后验参数值\( \mathbf{w}_{MAP} = \mathbf{m}_N\),当先验的方差无穷大时,即\( S_0 = \alpha^{-1} \mathbf{I}, \alpha -> 0 \)时,后验分布的均值就退化成了最大似然估计值。类似地,当N=0时,后验分布就退化成了先验分布。当数据点是一个接一个获得时,上次计算得到的后验分 布就可以作为下次计算时的先验分布,从而达到顺序计算的效果。
如果假设先验分布是一个零期望等方差的正态分布,那么其形式可以表示为
\[ p(\mathbf{w}) = N(\mathbf{w} | 0, \alpha^{-1} \mathbf{I}) \]
\[ m_N = \beta S_N \Phi^{T} \mathbf{I} \]
\[ S_N^{-1} = \alpha \mathbf{I} + \beta \Phi^{T} \Phi \]
根据贝叶斯定理,后验分布的对数可以表达为似然的对数,加上先验分布的对数,最终形成一个参数\( \mathbf{w} \)的函数,其形式是一个带规则化项的误差函数,其规则化项前的系数为\( \lambda = \alpha / \beta\)。
\[ ln p(w|t) = -\frac{\beta}{2} \sum_{n=1}^{N} (t_n - w^T \phi(x_n))^2 - \frac{\alpha}{2} w^T w + const \]
一般化的正态先验
\[ p(w|\alpha) = [\frac{q}{2} (\frac{\alpha}{2})^{1/q}]^M exp(-\frac{\alpha}{2} \sum_{j=1}^{M} |w_j|^q) \]
预测分布
在得到了参数的后验分布之后,我们并不做实际做些什么,真正要得到的是预测分布,即结合参数的后验分布来为新的输入做出合适的预测值。
\[ p(t|\mathbf{t},\alpha,\beta) = \int p(t|\mathbf{w},\beta) \dot p(\mathbf{w}|\mathbf{t},\alpha,\beta)dw \]
其中忽略了输入向量\(x\)以简化表达式。可以发现这个等式的右侧实际是两个正态分布的卷积,因而其结果也是一个正态分布,其期望和方差分别为
\[ \mu = \mathbf{m}_{N}^{T}\mathbf{S}_{N} \mathbf{\phi}(x) \]
\[ \sigma^2_{N}(x) = \frac{1}{\beta} + \phi^{T} (x) \mathbf{S}_{N} \phi (x) \]
期望值即为参数后验的期望与输入向量的内积;而方差值则可以分为两项,前者为数据噪声所引起的波动,而后者则可以看作参数值\( \mathbf{w} \)的波动,二者是独立可累加的。可以证明方差值是随着N值的变大而递减并趋向于0的,当样本足够大时,预测值的波动仅由训练数据中的噪声所带来。
预测分布的方差在训练数据点的附近最小,因而当数据点足够多时,预测分布的波动性也随之降低。
更一般地,如果参数\(w, \beta\)都被看作未知的,那么共轭先验就应该是一个Gaussian-gamma分布,而对应的预测分布就是一个学生t分布。
Equivalent Kernel
预测分布在一个点上的预测期望值可以表示为
\[ y(\mathbf{x},\mathbf{m}_{N}) = \mathbf{m}^{T}_{N} \mathbf{\phi}(\mathbf{x}) = \sum_{n=1}^{N}k(x, x_n)t_n\]
其中定义函数
\[ k(x,x') = \beta \phi(x)^{T} \mathbf{S}_{N}\phi(x') \]
这个函数称为平滑矩阵或者equivalent kernel,而回归函数可以表达为训练数据响应值的线性加权,因而被称为线性平滑。特别地,当待预测点距离某训练数据点近时,该点的响应时对应的权重就高,反之则小(核函数的局部属性)。
可以观察两个待预测点的预测方差之间的关系
\[ cov(y(x), y(x')) = cov(\phi(x)^{T} w, w^{T} \phi(x')) = \phi(x)^{T} \mathbf{S}_N \phi(x') = \beta^{-1}k(x,x')\]
其中cov是相对于w来说的。上式说明,在输入空间中相邻的两个点的预测期望值相关性较大,相反地,相距较远的两个点之间则相关性较小。
核函数给了我们一种新的思路,即不通过定义基函数和回归来实现预测,而是定义一个核函数,并使用训练数据的输出做线性加权而得到。(高斯过程)
该核函数还满足归一化的性质,但是并不保证其中的每个子项都非负。
\[ \sum_{n=1}^{N} k(x,x_n) = 1\]
另外还有一个核函数都满足的特征(不限于Equivalent Kernel),它们都可以表达为非线性函数的乘积的形式
\[ k(x,z) = f(x) f(z)\]
\[f(x) = \beta^{1/2} \mathbf{S}^{1/2}_{N}\phi(x) \]
PRML Notes - 3.2 Bais-Variance Decomposition
在第一章中,我们把回归问题分解为两个部分:推演和决策。假设推演步骤已经完成,即后验分布\( p(t|\mathbf{x})\)已经得到,接下来就需要选择一种损失函数,并以最小化损失为目的进行决策的步骤。一种常用的损失函数为平方损失(注: 请明确区分推演过程中使用的平方误差与决策步骤中使用的平方损失),在此条件下,最优预测值是通过以下条件期望得到的
\[ h(\mathbf{x}) = E[t|\mathbf{x}] = \int t p(t|\mathbf{x}) dt \]
平方损失可以写为以下形式
\[ E[L] = \int (y(x) - h(x))^2 p(x) dx + \int (h(x) - t)^2 p(x, t) dx dt \]
其中,第一项表达我们得到的预测与最优预测之间的差异,而第二项则表达了最优预测与真实响应值之间的差异,这项实际是以噪声引起的,是我们是不可控的。理想情况下,我们的预测与最优预测一致,这样就完全去掉了第一项,从而最小化平方损失。
实 际中,这个最优预测\( y(\mathbf{x}) = h(\mathbf{x}) \)是无法得到的,因为它的计算需要无限多的数据,而我们只有有限个数据点。因此,我们只能寄望于先找到一个模型\( y(\mathbf{x}, \mathbf{w}) \),再通过训练得到最优参数以最大程度的接近于\( h(\mathbf{x}) \)。
由 于数据是有限的,因此通过这些数据来训练而得到的模型是具有不确定性的。从贝叶斯的角度来看,这种不确定性是通过参数\( \mathbf{w} \)的分布来表达的。而在频率框架下,最终得到的并不是一个关于参数的分布,而是一个关于参数的点估计。不同的数据样本对应不同的参数点估计值,其不确定 性表达为不同数据训练造成的参数的波动以及损失值的波动,亦即
\[ E_D[(y(\mathbf{x}; D) - h(\mathbf{x}))^2] = (E_D[y(\mathbf{x}; D) - h(\mathbf{x})])^2 + E_D[(y(\mathbf{x}; D) - E_D[y(\mathbf{x}; D)])^2] \]
其中,第一项表达了该模型的平均预测与最优预测的差异(bias),而第二项则表达了该模型预测值自身的方差(variance)。结合前两个表达式,我们可以得到以下等式关系
\[ expected\_loss = (bias)^2 + variance + noise \]
我 们希望最小化损失值,但是实际上我们将不得在bias和variance之间做出权衡。当我们选用了一个非常复杂灵活的模型时,它能够很有效地降低 bias,却引入了较大的vairance;相反地,如果我们选用了一个严格的模型,它的variance较低,但是却引入了bias风险。最优的模型选 择就是找到bias和variance之间的一个最优点。
这个Bias-Variance Decomposition在实际中应用价值并不大,因为它需要计算\( E_D \),而这是不可能的。理论意义上,这个分解式还是给我们带来了一些insightful ideas.
PRML Notes - 3.1 Linear Basis Function Model
书中第三章的标题是Linear Model for Regression,即线性回归模型。线性模型的定义是相对于“未知参数”的线性函数。也就是说,虽然下面这个模型可以称为线性模型(实际上是最简单的线性模型,因为它不仅相对于未知参数是线性的,而且相对于输入变量也是线性的),但是其实际的定义要宽泛得多,因而才有了本节介绍的“线性基函数”模型。
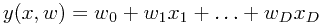
回归问题
给定训练数据集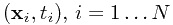 ,其中
,其中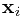 为D维变量,
为D维变量,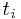 为响应值。
为响应值。
最简单的方法,我们希望通过数据得到一个响应值估计函数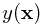 ,从而可以对未来的输入变量进行响应值预测。从概率的观点来看,我们要得到的不仅是一个输入变量的单点估计值,而是一个条件分布
,从而可以对未来的输入变量进行响应值预测。从概率的观点来看,我们要得到的不仅是一个输入变量的单点估计值,而是一个条件分布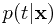 ,从而可以表达其响应值的不确定性。得到这个分布,实际我们就完成了“推演”的工作,“决策”步骤中,我们需要定义一个误差函数(比如第一章中提到的平方误差),再以最小化期望误差为目的来决策每个输入变量的响应值(在平方误差下,这个“决策”是响应值t的条件期望值)。
,从而可以表达其响应值的不确定性。得到这个分布,实际我们就完成了“推演”的工作,“决策”步骤中,我们需要定义一个误差函数(比如第一章中提到的平方误差),再以最小化期望误差为目的来决策每个输入变量的响应值(在平方误差下,这个“决策”是响应值t的条件期望值)。
基函数(basis function)
相比于最开始提到的那个“最简单”的线性模型,更一般的线性模型可以表达为
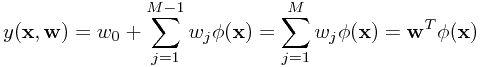
其中所有的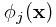 都称为基函数。特别地,
都称为基函数。特别地,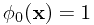 以容许
以容许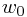 对函数的值产生一定的偏移(bias)。基函数的作用可以表现的预处理(如特征抽取)上,如PCA,MDS等经典的特征抽取算法都是以原坐标为基础进行线性组合,形成新坐标,再把数据表示的新的坐标下,以图可以更好地发现数据中的规律(例如PCA是把数据中方差最大的方向作为新的坐标体系)。而数据在新坐标体系下的坐标值就可以用这M个基函数来表示。
对函数的值产生一定的偏移(bias)。基函数的作用可以表现的预处理(如特征抽取)上,如PCA,MDS等经典的特征抽取算法都是以原坐标为基础进行线性组合,形成新坐标,再把数据表示的新的坐标下,以图可以更好地发现数据中的规律(例如PCA是把数据中方差最大的方向作为新的坐标体系)。而数据在新坐标体系下的坐标值就可以用这M个基函数来表示。
虽然是作用于线性模型中,基函数并不必须是线性函数,从而极大地扩充了最简单线性模型的表达能力。多项式模型就是非线性基函数的一个实例。
spline function:非输入变量的全局函数,因此可以把输入空间划分成独立的部分,一部分的变化不会影响其它部分(不懂,待研究)
除多项式基函数外,其它一些基函数的例子包括
-
Gaussian基函数:
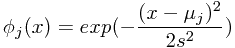
-
sigmoidal基函数:
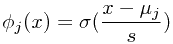 ,其中
,其中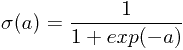
-
tanh基函数:
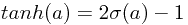 ,因此sigmoidal基函数的线性组合也是tanh基函数的线性组合
,因此sigmoidal基函数的线性组合也是tanh基函数的线性组合 - Fourier基函数:晕
极大似然法和最小二乘法
假设响应值t是由一个以x为输入的确定的函数加上一个高斯噪声而得到的,即
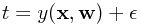
其中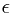 是符合正态分布
是符合正态分布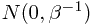 的噪声变量。那么我们希望得到的条件分布可以写作
的噪声变量。那么我们希望得到的条件分布可以写作
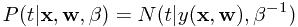
如果假设我们在决策时所选的误差函数就是平方误差,那么决策函数就是以上分布的条件期望,即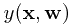 。
。
这里需要注意的一点是,高期噪声假设在多峰值的场景下是不适合的。
假设给定的N个数据是独立同分布的(iid),那么对数似数函数可写作
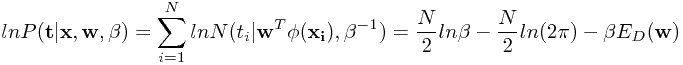
其中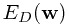 为Sum-of-square误差函数(请参见第一章)。当我们使用求导的方法来计算参数
为Sum-of-square误差函数(请参见第一章)。当我们使用求导的方法来计算参数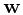 时会发现,正如第一章所述,由于表达的前两项没包含
时会发现,正如第一章所述,由于表达的前两项没包含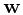 ,因此对ML和LS求导实际是等价的。
,因此对ML和LS求导实际是等价的。
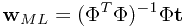
这个等式称为最小二乘问题的正规式(normal equations)。而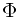 是一个N*M阶的矩阵,其中
是一个N*M阶的矩阵,其中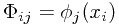 。 等号右侧除t之外的部分称为矩阵
。 等号右侧除t之外的部分称为矩阵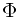 的伪逆矩阵,可以看作是非方阵的逆阵。特别地,当
的伪逆矩阵,可以看作是非方阵的逆阵。特别地,当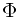 是方阵时,伪逆阵等于逆阵。
是方阵时,伪逆阵等于逆阵。
下面对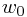 的意义做深入探索。对
的意义做深入探索。对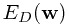 稍作变形,可得
稍作变形,可得
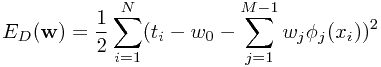
再对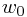 对导数,可解得
对导数,可解得
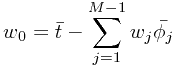 ,其中
,其中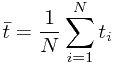 ,
,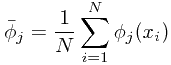 。
。
因此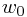 可以解释为训练集中平均响应值,与训练集平均基函数值的加权平均之间的差。
可以解释为训练集中平均响应值,与训练集平均基函数值的加权平均之间的差。
同样地,对极大似数函数相对于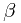 进行求导,可得参数值为
进行求导,可得参数值为
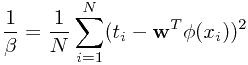
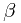 从上式中可解释为响应值围绕着回归函数值的波动程度,这也与其开始的定义“噪声方差”相一致。
从上式中可解释为响应值围绕着回归函数值的波动程度,这也与其开始的定义“噪声方差”相一致。
最小二乘法的几何解释
如果把响应值$$t = (t_1, t_2, ..., t_n)$$看作n维空间中的一个向量,同时将每个基函数应用于所有\( x_i, i=1...n \)形成M个基函数向量$$\bar {\phi_j}, j=1...M$$的话,最小二乘法在几何意义上就可以解释为M个基函数向量形成的线性子空间中找到一个最优向量,使其与响应向量的欧氏距离最小。
进一步地,这个最优向量实际就是响应向量在这个基函数向量所形成的子空间中的投影,最优解就是基于M个基函数向量线权加权得到这个最优向量时的参数\( w, \beta\)。
在线学习
如果训练数据集非常大,那么使用其对模型进行一次训练可能是极其耗时的,此时使用在线学习(或者流式学习)算法将是一种更好的选择。在这种场景下,我们让数据一个接着一个地使用,当每获取一个数据点时,就基于这个新的数据点来更新模型的参数值。
我们可以采用一种称为随机梯度下降的方式来实现在线学习。具体地,如果n个数据点的误差函数可以表示为
\[ E = \sum_n E_n \]
那么当第n个点到来时,模型参数的更新方式为
\[ \mathbf{w}^{(\tau + 1)} = \mathbf{w}^{(\tau)} - \eta \delta E_n\]
其中\(\eta\)为学习率,\(\tau\)为迭代次数。参数的初始值可以随机选。特别地,对平方误差函数,上式可表示为
\[ \mathbf{w}^{(\tau + 1)} = \mathbf{w}^{(\tau)} - \eta (t_n - {\mathbf{w}^{(\tau)}}^T \phi_n ) \phi_n \]
这个算法被称为LMS(least-mean-square)算法。
带有规则化项的最小二乘法
为了控制过拟合的出现,第一章中提到一种利用规则化项的方法,即最小化带有惩罚项的误差函数
\[ E_D(\mathbf{w}) + \lambda E_W(\mathbf{w})\]
其中\( \lambda \)为规则化项系数,用以控制两者之间的权衡关系。一种简单的规则化项称 二次规则化项,称为权重衰减,即
\[ E_W(\mathbf{w}) = \frac{1}{2} {\mathbf{w}}^{T} {\mathbf{w}}\]
如果将原始误差替换为平方误差,那么整个误差函数就可以表示为
\[ \frac{1}{2} \sum_{n=1}^{N} (t_n - \mathbf{w}^T \phi(x_n))^2 + \frac{\lambda}{2}{\mathbf{w}}^T {\mathbf{w}} \]
基于以上误差函数,通过最小二乘法得到的最优参数值为
\[ \mathbf{w} = (\lambda \mathbf{I} + \Phi^{T} \Phi)^{-1} \Phi^{T} \mathbf{t}\]
实际上,其就是对最小二乘结果的一个简单扩展。
更加一般的规则化项可以表达为
\[ \frac{1}{2} \sum_{j=1}^{M}{|w_j|}^{q}\]
其中当q=2的时候,即为权平方的规则化项。当q=1时,这个带规则化项的最小二乘法也称为套索(lasso),当\( \lambda \)足够大时,它可以产生一个稀疏的模型,即让多数基函数对应的系数接近于0.
本质上,规则化项方法并没有从根本上解决过拟合问题,或者模型复杂度问题,它仅仅是将问题做了转移,从寻找合适数量的基函数,变为了如何确定规则化项系数\( \lambda \)。
本章下面内容均假设规则化项为二次规则化项。
多维响应值
一些情况下,每个\( x_n \)所对的输出\( t_n \)并不是一维的,而是多维的。最简单的方式就是为每一个响应维度确定一组基函数,从而把问题分解为多个线性回归问题。当然,也可以选择一组相同的基函数,来应付所有的响应维度。
\[ p(\mathbf{t} | \mathbf{x}, \mathbf{W}, \beta) = N(\mathbf{t} | \mathbf{W}^T \phi(\mathbf{x}), \beta^{-1}\mathbf{I}) \]
同样通过最小二乘法来求解,可得
\[ \mathbf{W_{ML}} = (\Phi^T \Phi)^{-1}\Phi^T\mathbf{T}\]
而每响应维度上,其对应的参数值为
\[ \mathbf{w_k} = (\Phi^T \Phi)^{-1}\Phi^T \mathbf{t_k}\]
因此,我们可以将响应维度进行解耦,我们只需要计算一次\( \Phi \),然后就可以计算任何一个维度上的参数值。>
更一般地,正态分布的协方差阵可以不是严格对角阵,而可以是任意矩阵,我们同样可以对每个响应维度进行解耦。这是因为\( \mathbf{W} \)是只与分布的均值相同,而其估计值是可以独立于协方差来估计出来的,即它是独立于协方差的。(详见第一章)