[PGM] Section 7. Inference-Variable Elimination
上一节提到的Conditional Probability Query和MAP中最关键的点就是要算贝叶斯公式中的分子,这个有了之后要么归一化要么取最大值,这事就搞定了。所以本节的这个VE算法就是用来算这个分子的。
Variable Elimination Algorithm
这个算法超级简单,就是每一步都尝试去掉其中的一个变量,方式是把所有与这个变量相关的factor都搞在一起,然后marginalize,生成的结果记作一个新的factor;然后选择另一个变量去重复上面的步骤,直至所有无关变量会都被eliminate掉了,这个事也就搞定了。直接给个例子,我们想算下面这个BN中P(J)的分布:
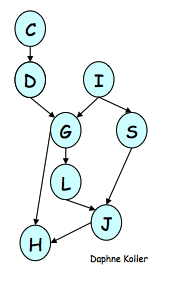
先把P(J)写成factor product的形式
\[\hat P(J) = \sum_{L,S,G,H,I,D,C} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_G(G, I, D) \phi_H(H, G, J) \phi_I(I) \phi_D(C, D) \phi_C(C)\]
假设我们按照C, D, I, H, G, S, L的顺序来依次做variable elmination,先来搞C,把所有跟C相关的factor放在一起,并把对C的求和push进去,形成
\[\hat P(J) = \sum_{L,S,G,H,I,D} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_G(G, I, D) \phi_H(H, G, J) \phi_I(I) \sum_C \phi_D(C, D) \phi_C(C)\]
重新定义一个新的factor,\(\tau_1(D) = \sum_C \phi_D(C, D) \phi_C(C)\),代进去,得到
\[\hat P(J) = \sum_{L,S,G,H,I,D} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_G(G, I, D) \phi_H(H, G, J) \phi_I(I) \tau_1(D)\]
这样我们就成功把C去掉了,或者说marginalize C。下一步要去掉是D,同样的定义\(\tau_2(G, I) = \sum_D \phi_G(G, I, D)\tau_1(D)\),代入上式中得到
\[\hat P(J) = \sum_{L,S,G,H,I} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_H(H, G, J) \phi_I(I) \tau_2(G, I)\]
这样D也被干掉了。后面的工作以此类推,直到把等式右边非J的变量都干掉了,计算就结束了,我把最后一步写出来。
\[\hat P(J) = \sum_{L,S} \phi_J(J,L,S) \tau_5(L, J, S)\]
如果有Evidence咋办?凉拌!
\[\hat P(J, I=i, H=h) = \sum_{L,S,G,D,C} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I=i) \phi_G(G, I=i, D) \phi_H(H=h, G, J) \phi_I(I=i) \phi_D(C, D) \phi_C(C)\]
就这么简单!
贝叶斯公式的分子算完了,如果想得到\(P(J|I=i, H=h)\)呢?正如前面所述,renormalize就可以了,归一化常量就是\(P(H=h, I=i)\)。
前面这个例子是BN,对MN其实也一样,都是对factor做处理,就不多费话了。
再来两张图,总结一下VE算法的关键步骤:


简单来说,把所有与变量Z相关的facor乘在一起,通过marginalize把Z干掉,得到的结果变成一个新的factor参与到下次的计算中;重复以上步骤即可。
Complexity Analysis
这部分是对VE算法的复杂度分析,比较无趣,但是跟后面的知识也有些关联,还是得写写。
VE算法执行的每一步由两部分组成:factor product + marginalization。先来看看每部分的有哪些工作量。
\[\psi_k(X_k) = \Pi_{i=1}^{m_k} \phi_i\]
这个是factor product的步骤,它把\(m_k\)个factor相乘。对于\(X_k\)的每一个assignment,需要每个factor都参与相乘,因此共有\(m_k - 1\)次乘法操作。而\(X_k\)有多少assignment呢?记这个数为\(N_k = |Val(X_k)|\),于是这个factor product的步骤需要\((m_k-1)N_k\)次乘法。
\[\tau_k(X_k - \{Z\}) = \sum_Z \psi_k(X_k)\]
这个是marginalization的步骤,令\(N_k\)的定义不变,由于\(X_k\)的每一个assignment都要参与且仅一次参与marginalization求和的操作,因此这步需要花费掉\(N_k\)个加法操作。
ok,现在来看整个算法执行过程中的花费。假设有n个变量,m个factor(对于BN来说,m<=n,因为每个变量都有一个factor,如果算上evidence,那么有m<n的可能;而对于MN,通常有m > n,因为MN的factor可能是多个变量的组合,如pairwise factor)。在VE的每一次eliminate时,算法会生成一个新的factor,同时会eliminate至少一个变量。我们一共只有n个变量,所以至多会有n个eliminate的步骤,而总的factor数量\(m^* <= m + n\),这里小于就是因为至多n次eliminate而生成新factor。
取VE执行过程中最大的factor的assignment数量为\(N = max(N_k)\),于是
- Product operations: \(\sum_k (m_k-1)N_k <= N\sum_k(m_k-1)\),而由于每个factor最多只参与一次factor product就被融入新生成factor之中了,所以上式至多为\(Nm^*\);
- Sum operations: \(\sum_k N_k <= N*n\),因为至多只有n次elimination操作。
这样看来,所有的花费相对于N, m, n都是线性的,但是N实际上相对于变量个数是指数级的,所以我们白高兴了。
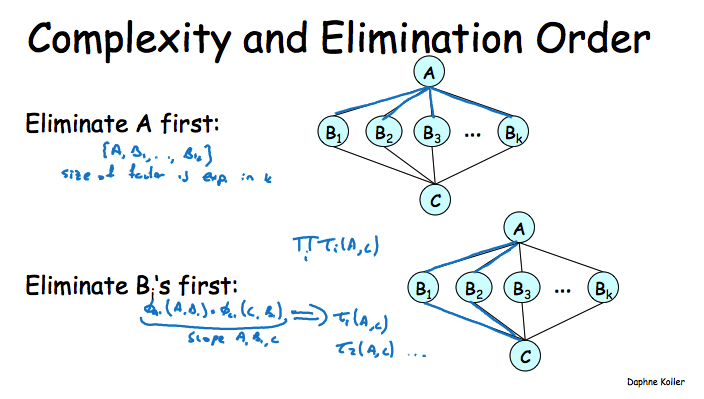
从上面这些分析来看,m和n不可变的情况下,我们要尽量不要在VE的执行过程中生成太大的factor,因为在变量的cardinality不可变的情况下,我们只能让factor不要包含太多的变量。而从一些例子中可以发现,Elimination Order对于控制N有着很大的作用,举一个比较极端的例子,下图中先去掉A时会生成一个包含k个变量的factor,而先去掉各个B时,生成factor只会包含2个变量。
Graph-Based Perspective
这一小节的内容核心是Induced Graph,先给出定义,然后再给例子。
定义于factors \(\Phi\)和elimination order \(\alpha\)的Induced Graph \(I_{\Phi, \alpha}\)满足:1. 无向图;2. 如果两个变量\(X_i, X_j\)在按照\(\alpha\)来执行VE过程中出现在同一个factor中,而且原图上不存在边的话,那么它们之间就被连上一条filling edge。
换句话说,原图由于VE按照某种顺序执行过程而添加上一些边,这个生成的新图就是Induced Graph。原图是啥呢?就是由factors induce出来的MN,这个前面的章节里已经提过了。
下面给例子,先是原图,这个是通过BN->factors->MN来得到的。
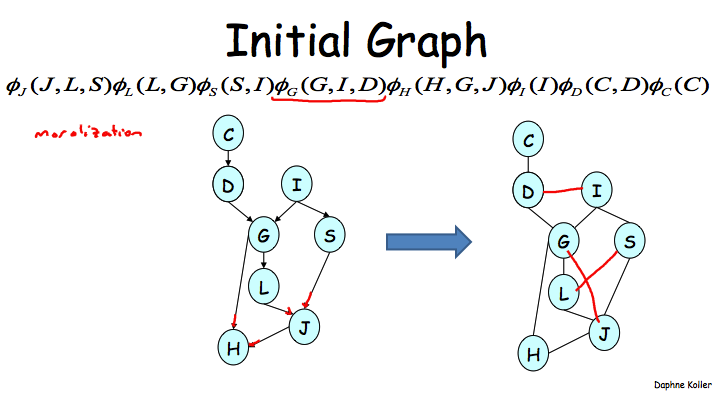
如果按照C, D, I的顺序来执行VE的话,那么干掉I之后就需要在G和S之间添加上一条边了,因为它们会同时出现在一个新的factor之中。
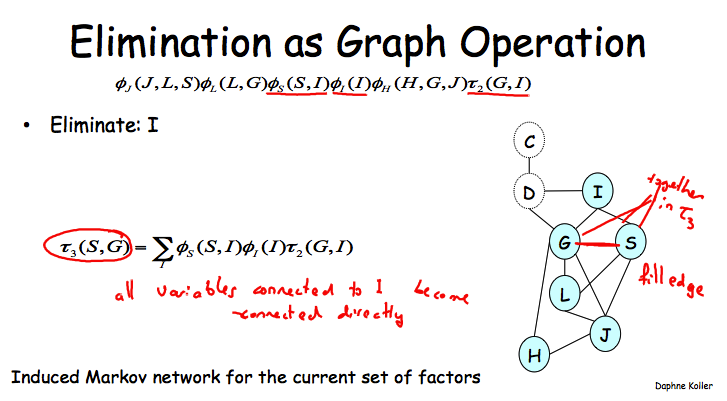
这个图跟VE的复杂性有啥关系吗?必须有!
Theorem: Every factor produced during VE is a clique in the induced graph.
clique就是一个maximal fully connected subgraph,也就是任意两个结点之间都一条边相连,而添加任意一个其实变量都不能使这个条件满足。结合clique的概念,其实上面这个定理很好理解,之所以生成一个新的factor是由于我们把与某个变量Z相连的所有factor都搞到一起了,而生成新的factor之后,Z的邻居们也肯定都有边相连(没有的都会被补上filling edge)。因为我们已经把Z的所有邻居都找来了,任意一个非Z邻居的变量都不可能加入这个clique,因为它至少无法与Z相连。
Theorem: Every clique in the induced graph is a factor produced during VE.
这个也很好理解,先给定出组成一个clique的K个变量,那么肯定会有一个变量在VE的过程中首先会被eliminate掉。因为在eliminate之后就不可能再有其它结点能与之相连了,所以此时它应该已经与clique中其它的K-1个变量都直接相连了。而在eliminate之后生成的新factor中,这K-1个变量必须都在其中,因此它们之间都会有边相连形成fully connected,所以此时这个clique就已经形成了。
然后就是Induced Width的概念:这个值就是Induced Graph中最大的clique的包含的结点个数-1。为啥减1呢?因为clique中实际是包含了被eliminate掉的那个变量,而生成的新factor则不包含这个变量,而前面一个小节也提到了VE的执行效率很大程度上受制于VE过程中最大的factor包含的变量个数(记作factor size),所以这样就有Induced Width = factor size。
因此最小化factor size等价于最小化induced width,于是就有了minimal induced width的概念:\(min_{\alpha}(width(I_{K, \alpha}))\);它实际上就直接对应了一个VE算法执行效率的下界。
Finding Elimination Orderings
Theorem: 对于一个图H,判断是否存在一个elimination ordering使用得induced width <= k还是一个NP-complete问题。这日子没法过了!
另外注意的是,这个NP-hardness与inference问题的NP-hardness是独立的,也就是说,即使给出了一个最优的ordering,用它去做inference也同样是指数级的。
好吧,既然如此,我们只能求助于Greedy Search方法了,即每个步都优先干掉最小cost的那个变量,咋定义cost呢?
- min-neighbors: 当前图中的邻居数量
- min-weight: 新生成的factor的assignment数量
- min-fill: 最小数量的filling-edge,讲师说这个function效果好
- weighted min-fill: 新的filling edge的weight之和,每边edge的weight为其相联的两个node的weight的乘积。
Theorem: The induced graph is triangulated – No loops of length > 3 without a “bridge”。这个定理不知道干啥用的,后面也没讲。。。
最后Robot Localization的例子,在这个MN中先eliminate landmards还是poses会形成两个密度差异很大的induced graph,而密度越大说明对应的factor包含的变量越大,VE执行起来也就越慢。
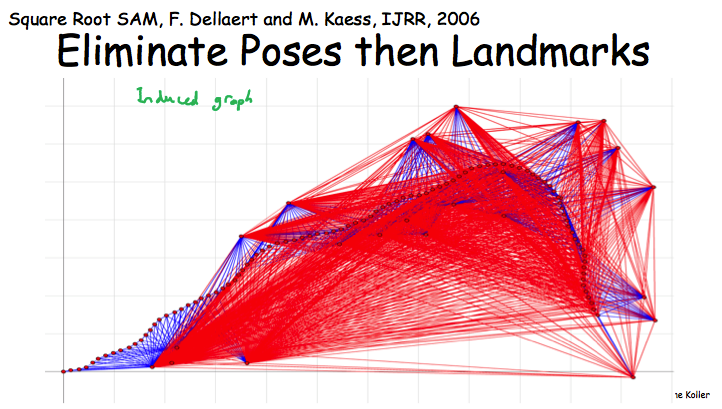
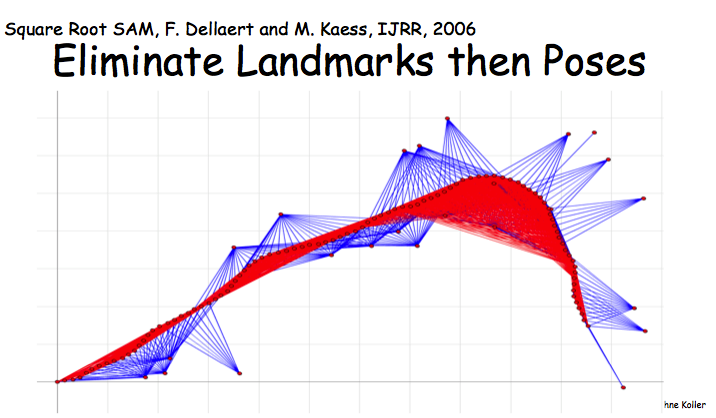
[PGM] Section 6. Inference-Overview
前面都是讲PGM的representation,从这里开始,后面讲的是Inference,即当我们有了一个完整的PGM之后,如何使用它来回答一些问题。这一小节就是在说有哪几种类型的“问题”。
Conditional Probability Queries
说白了,就是在给定一个PGM的情况下,要算\(P(Y|E=e)\)的概率分布是啥;其中E=e称为Evidence,也就是已知的某些变量的取值,而Y为Query,也就是我们的目标变量。
不幸的是,给定一个PGM \(P_{\Phi}\),一个变量X及其某个取值x,想要计算其概率\(P(X=x)\)或者判断是否满足\(P(X=x) > 0\)都是NP-hard;更不幸的是,即使我们降低要求,只想要一个近似解,那么这个问题也是NP-hard。万幸的是,这些都只是worst case,对于general case还是有希望能得到efficient solution的。
计算Conditional Probability Query的通用方式称为Sum-Product,在介绍之前需要先声明一下:后面所有的操作都是针对factor来做的,对于MN这样毫无问题,因为factor原来就是MN的component;而对于BN,其原始component是条件分布\(\hat P(X|Par_X)\)(注意这里是unormalized measure),所以需要做一个定义,即\(\phi(X, Par_X) = \hat P(X|Par_X)\),这样BN也可以使用factor来表示了。
Sum-Product实际上工作就是把所有的factor做product,然后marginalize所有无关变量,比如说像下面这个BN中计算\(P(J)\)例子:
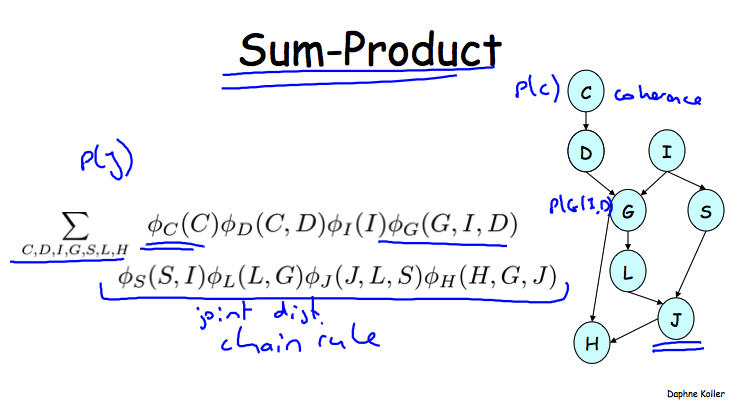
这里忽略了一点,就是这里没有Evidence。如果要计算的是\(P(J, D=d)\)怎么办?很简单,实际就是直接把D=d代入到上面那个等式中,变成了
\[P(J, D=d) = \sum_{C,I,G,S,L,H} \phi_C(C) \phi_D(C, d) \phi_I(I) \phi_G(G, I, d)...\]
这里需要注意一点,通常factor product出来的是\(\hat P\)而不是\(P\),需要再normalize,这个例子是BN,它的factor对应条件概率分布,也就没有这个问题了。
\(P(J, D=d)\)是算出来了,但是它不是Conditional Probability Query啊,我们的任务是计算形为\(P(J|D=d)\)的分布吧?下面给出通用步骤。
定义Y为目标变量,E=e为Evidence,令\(W = \{X_1,...,X_n\} - Y - E\),即余下的所有变量,有如下等式
\[P(Y|E=e) = \frac{P(Y, E=e)}{P(E=e)}\]
这个就是贝叶斯公式
\[P(Y, E=e) = \sum_W P(Y, W, E=e) = \sum_W \frac{1}{Z} \Pi_k \phi_k(D_k, E = e) = \sum_W \frac{1}{Z} \Pi_k \phi^{'}_k(D^{'}_k)\]
这个其实就是上面那个Sum-Product+Renormalize
\[P(E = e) = \sum_Y P(Y, E=e)\]
把后面那个两个计算式代入贝叶斯公式,发现归一化常量Z是可以被约掉的,所以我们要做的其实就是计算\(\sum_W\Pi_k \phi^{'}_k(D^{'}_k)\),也就是Sum-Product,然后再做一次renormalize就完事了。注意这里的renormalize使用的归一化常量跟上面第二行公式后注的那个不一样。
计算条件概率的算法有很多,课件中列了一些,在后面课程中都会讲到,包括Variable Elimination,Message Passing以及Random Sampling instantiations。
MAP Inference
这个是第二类问题,给定Evidence E=e,希望能得所有其它变量Y的一个conherent assignment y,使得\(P(Y=y|E=e)\)最大。应用场景包括Message decoding(最可能的原信息),Image segmentation(superpixels上最可能的label assignment)。
MAP is not equal to Max over Marginals! 其实这是句费话,学过点概率统计的应该都知道。
不幸的消息又来了,找使用\(P(X)\)最大的x也是NP-hard问题,甚至于判断\(P(x) > p\)是否成立也是NP-hard的。好在它仍然只在worst case下成立,在average case下还是有希望的。
与Sum-Product相对应的,解决MAP问题使用的方式是Max-Product,而且计算更简单。根据前面写的贝叶斯公式,我们知道选择最优的y只需要考虑分子,因为分母是与Y无关的,而进一步地
\[P(Y, E=e) = \frac{1}{Z} \Pi_k \phi^{'}_k(D^{'}_k) \propto \Pi_k \phi^{'}_k(D^{'}_k)\]
最后一步同样是因为,归一化常量并不影响y之间的相对大小,因此可以忽略。于是我们要得到的就是让最后一个表达式最大的y。
解决MAP的算法也列出一些:Variable Elimination, Message Passing, integer programming, graph-cut method(for some networks), combinatorial search。
[PGM] Section 5. Representation-Markov Networks
Pairwise Markov Networks
前面的讲的Bayesian Network是有向图,这节说的Markov Networks是无向图。从最简单的pairwise的case说起。
有向图的局部结构所表达的意义很明确,比如从A到B的结构,表示的就是\(P(B|A)\),而无向图则因为没有方向的概念,它就没有直接且有意义的概率分布来表示,所以只好用factor的概念来做抽象描述。
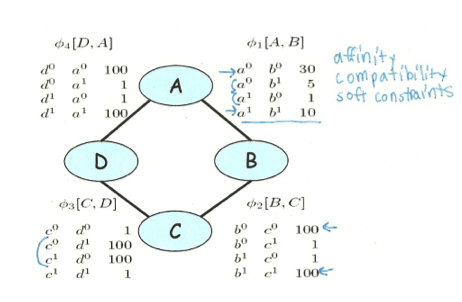
(我发现我越来越懒了,各种截图)
上面是一个例子,每个变量取值非零即一,而每条边上对应的factor,比如\(\phi (A,B)\)就表示这两个变量在各种取值下的权重,这里A和B取值相等时权重更高,表示这两个变量是比较正相关的。但是需要注意的是,每个factor都只是一个局部信息,它不会直接对应到我们最终得到的联合概率分布,甚到不能直接对应到与这两个变量相关的边缘分布或者条件分布上。这一点与Bayesian Network非常不同,用后面的例子一看就清晰了。
在有了这些factors之后,我们想要算这些变量的联合分布,做法就是直接利用factor product(如下),然后normalize一下就哦了。
\[ P(A,B,C,D) = \phi_1(A,B) * \phi_2(B,C) * \phi_3(C,D) * \phi_4(A,D)\]
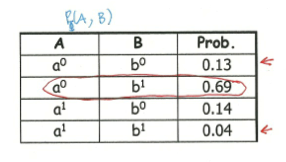
有了联合分布,自然可以算出一个边缘分布来,上面这个表格就是计算出来的\(P(A,B)\),对比一下包含局部信息的\(\phi(A,B)\),可以发现两者有天壤之别。原因就在于前面关于A和B的整体信息(实际上是受了C,D之间强烈取值不一致权重高的影响),而后者只是局部信息。
下面就是Pairwise Markov Networks的定义:一个包含结点\(X_1,...,X_n\)和边\(X_i, X_j\)的无向图,每条边上都有一个\(\phi_{ij}(X_i, X_j)\),这个东西就是Pairwise Markov Networks。这里的Pairwise体现在,每个factor的domain只有两个变量。
General Gibbs Distribution
书接上回,前面提到了Pairwise的case中,每个factor中只涉及两个变量,它的表达能力足够了吗?我们考虑一个fully connected的pairwise MN,即任意两个变量之间都有一个factor,假设共有N个变量,且每个变量可以有d个取值,那么这些factor的product可以产生的组合数就是\(O(n^2d^2)\),而实际上这N变量的联合概率分布应该是有\(O(d^n)\)个组合,二者之间还有有很大差距,这说明pairwise MN的表达能力并不足够。
为解决这个问题,就有人提出了Gibbs Distribution的概念,即定义一些General Factor \(\phi_i(D)\),其中每个D可能包含一个或者多个变量(而不是pairwise中的2个变量),把这些factors集中在一起表示为\(\Phi = {\phi_i(D_i)}\),后面的就都一样了,factor product+normalization,不费话了。所以实际上Gibbs Distribution所做的就是对每个factor的domain中的变量个数扩展到了任意个,同样的问题,这样表达能力就足够了吗?必须的,因为定义一个包含所有变量的factor都是可行的。
但是这种一个factor中有多个变量的形式,如何对应到Markov Network上呢,这个图咋画呢?结论就是Induced Markov Network,即当存在一个\(\phi_m \in \Phi\),使得\((X_i, X_j) \in D_m\)时,就在这两个结点之间连上一条边,画上所有的这些边,就形成了Induced Markov Network。
有了分布P,又有个图H,那么就可以把BN的那套东西搞过来了。
首先是Factorizatioin的概念,当存在一个factor的集合\(\Phi\),使用得\(P = P_{\Phi}\)并且H是\(\Phi\)的Induced graph时,就说P factorizes over H。实际上就是以\(\Phi\)作为中介,把P和H联系起来了。因为不同的\(\Phi\)可能会生成相同的H,所以H并不能完整表达P中的信息。
Flow of Influence:这个比BN要简单得多,没有什么v-structure这么变态的东西,只有在两个变量之间有一条active trail(即这条路径上没变量是被observed),那就这条influence就是通的。而且,两个变量间influence可能有多条活跃路径。最后,这种influence只依赖于这个graph,不依赖于factors。
Conditional Random Field
这东西跟前面的Gibbs Distribution很类似但是归一化方式不同,这也造就了它独特的地方和应用场景,当在做某些预测Y的任务而不想关心X_i之间的关联时还是很有用的。
假设有一组变量\(X_1,...,X_n\),以及一个目标变量Y,我们想做就是找到从X到Y之间的条件分布\(P(Y|X)\),以帮忙我们通过观测到一系列X来预测未知的Y。在图像实体识别中,X可以是图像中的元素值,Y可以是object label;在文本处理的例子中,X可以是句子中的各个word,而Y则是POS tag。
CRF具体形式与Gibbs分布几乎就是一样的,给定\(\Phi\),然后利用factor product来得到unormalized measure,表示为\(\hat P\)。不同之处在于,后面归一化项(或者称为partition function)是不同的,如下
For Gibbs Distribution: \(Z = \sum_{X,Y} \hat P(X, Y)\)
For CRF: \(Z(X) = \sum_{Y} \hat P(X, Y)\)
前者归一化后得到的是联合概率分布\(P(X, Y)\),而后者得到的则是条件概率分布\(P(Y|X)\)。
这个玩意儿有什么用处呢?假设所有factors的形式都是\(\phi(X_i, Y)\),即没有任何的X变量之间的信息,如何我们使用这些factors来计算联合分布的话,实际上我们就做出了如朴素贝叶斯般的假设,即所有的X之间是独立的,显然这种假设在某些情况下是很粗暴的。而像前面提的这种通过X预测Y的场景下,X之间有啥关系我们是不关心的,我们只是想了解它们如何影响Y的取值,这种情况下利用CRF计算得到的条件概率分布就足够满足我们了,而不用去关心X之间会有什么联系。换个角度来说,前者计算出的联合分布实际是一个信息最全的分布,因为通过联合分布可以计算任意的条件分布和边缘分布,包括X之间的关联,但是有些信息我们实际是不关心的,也没有必要去model的;而条件概率分布虽然信息不如联合分布全(比如它就没有X之间关系的信息),但是对于我们的预测任务来说是足够的了。
课程中又提到CRF跟很多现有模型是有非常强的关联的,比如,Logistic Model就是CRF的一种特殊形式,很有意思,但是推导过程我就不写了,贴个图了事。

最后抄一句话做总结:CRF allows models with highly expressive features, without worrying about wrong independencies.
Independecies in Markov Networks
从这里开始会有一些很概念性的东西,虽然挺烦,但还是得写写。多数概念都是BN那边迁移过来的。
Seperation in MN: X and Y are separated in H given Z if there is no active trail in H between X and Y given Z.
I-Map:MN中的独立性集合表示为\(I(H) = {(X \perp Y| Z): sep_H(X, Y|Z)}\),如果P满足这个\(I(H)\),那么就说H是P的一个I-map。
Factorization => Indepedencies: If P factorizes over H, then H is an I-map of P. (If P factorizes over a graph H, we can read from the graph independencies that must hold in P (an independency map).)
Factorization <= Indepedencies: For a positive distribution P, if H is an I-map for P, then P factorizes over H.
我的一点理解是,H中的信息总是P的一个子集,P能够factorization不代表它所有的信息都能表达在H中。
I-maps and Perfect Maps
如果我们把一个概率分布P中所有的独立性约束都提取出来,表示为\(I(P)\),那么对于P的任意一个I-map来说,都有\(I(G) \in I(P)\),而反向则并不总是成立的。换句话说,G中的独立性约束总是P的一个子集,可能无法完整表达P中蕴含的信息。
当然,理想情况下,对于一个P,我们希望能得到一个能表达其完整的独立性信息的图G,因为这样的话,G中就包含了所有P中的独立性条件,图不但会更加informative,也会变得更加稀疏(因此也就会有更少的参数)。我们定义当满足\(I(G) = I(P)\)时,就称它为Perfect Map。
理想很丰满,但现实很骨感,对于一个P来说,想得到它的Perfect Map通常是很难的。举几个例子,
- 假设一个pairwise MN,而P是由它导出的一个包含其所有独立性信息的概率分布,我们希望得到一个BN的使其成为Perfect Map。事实证实,找不到这个样Perfect Map。
- 反过来,假设v-structure的BN,而P是由它导出的,我们希望能得一个包含Perfect Map的MN,事实证实,也是找不到的。
- 另外还有一个XOR的例子,我就不多说了。
前两个例子也说明,BN与MN之间的等价转换有时是不可行的,总是可能会丢失掉一些原有的信息。
更加让人崩溃的是,即使我们找到一个P对应的Perfect Map,也不能保证它是唯一的。比如,最简单BN模型,A->B, A<-B两个图的所表达的独立性信息就是相同的(实际都是空集);再比如,三个变量的情况,除了v-structure中的X->Y<-Z之后,另外的三种图也是表达了相同的独立性信息。当两个图G,H中所包含的独立性信息相同,即\(I(G) = I(H)\),那么就称二者是I-equivalent。多数图都有对应的很多I-equivalent变种。
Log-Linear Models
对于MN,除了使用factor product+normalize来表达联合概率分布外,还可以使用log-linear model来实现,表达式为
Factor Product: \(\hat P = \Pi_i \phi_i(D_i)\)
Log-linear Representation: \(\hat P = exp(-\sum_j w_j f_j(D_j)) = \Pi_j exp(-w_j f_j(D_j))\)
每个i表示factor的索引,每个\(D_i\)是相对于这个对应的factor来说的;相应地,每个j是feature的索引,所以\(w_j, D_j\)都是相对于这个feature的,也就是说每个feature会有一个对应的权重及它的scope。而不同的feature也可以有相同的scope。另外,需要注意一点,factor的scope和feature的scope甚至可以是不相关,因为feature和factor可以不存在一一对应的关系,从这个意义上讲,Log-linear Representation中的最后一个表达式中,每个\(exp(-w_j f_j(D_j))\)可以看作是重新定义的一个factor。
上面是两种不同的对联合分布的表示方法,所以需要首先证明Factor方式是可以等价地表达后Log-linear方式的。
假设有一个\(\phi(X_1, X_2), X_i \in {0, 1}\),这个factor的取值分别为\(a_{00}, a_{01}, a_{10}, a_{11}\),其中每个\(a_{ij} = \phi(X_1 = i, X_2 = j)\)。现在我们定义4个feature,分别为
\[f_1 = I\{X_1 = 0, X_2 = 0\}\]
\[f_2 = I\{X_1 = 0, X_2 = 1\}\]
\[f_3 = I\{X_1 = 1, X_2 = 0\}\]
\[f_4 = I\{X_1 = 1, X_2 = 1\}\]
其中I表示indicator function。于是,我们得到如下等式\(\phi(X_1, X_2) = exp(-\sum_k w_k f_k(X_1, X_2))\),其中\(w_k\)为对应的\(a_{ij}\)的对数的相反数。这4个feature的scope是相等的,也对应了前面所说的“不同的feature也可以有相同的scope”。
后面就是一些应用的例子了。
首先是对于单词的注标问题,X表示当前的单词,Y表示这个单词的label。基于对这个领域的理解,我们可以定义如下的features
\[f_1(Y, X) = I\{Y = B\_PER, X~is~capitalized\}\]
\[f_2(Y, X) = I\{Y = B\_LOC, X~appears~in~atlas\}\]
......
然后就可使用这些features去构建一个log-linear model,表达对应的联合概率分布\(P(Y, X)\)。
第二个例子是Ising Model,没听懂具体是干什么用的,它的结构是pairwise MN,每个变量\(X_i \in {-1, +1}\),定义两种features,一种是单变量的\(f_i(X_i) = u_i X_i\),另一种是双变量的feature,即\(f_{i, j}(X_i, X_j) = X_i * X_j\),其中\(f_{i, j}\)是说这个feature只会应用于\(X_i, X_j\)这两个变量上(scope),后面的内容会对它做扩展,这里先不管。对应的联合分布的表达式为
\[P(X) = exp(-\frac{1}{T} E(X))\]
\[E(X) = -\sum_{i<j} w_{ij} X_i X_j - \sum_i u_i X_i\]
最后一个例子是Metric MRF。一种被特别提到很常用feature称为metric,而它所对应的MN被称为metric MRF。在使用metric MRF的应用中,通常都希望相连的两个变量有相似的取值。
metric实际就是一个距离函数\(\mu : V * V \to R^{+}\),其中V是每个变量\(X_i\)的取值空间。这个距离函数要求满足三个基本属性:自反性,对称性以及三角不等式条件。
\[f_{i, j}(X_i, X_j) = \mu (X_i, X_j)\]
\[P(X) = exp(-\sum_{i, j} w_{i, j} f_{i, j}(X_i, X_j))\]
这样就满足了当有边相联的两个变量取值不相似(即距离较远时),它会拉低这个assignment整体的联合概率。
一些常用的metric函数定义
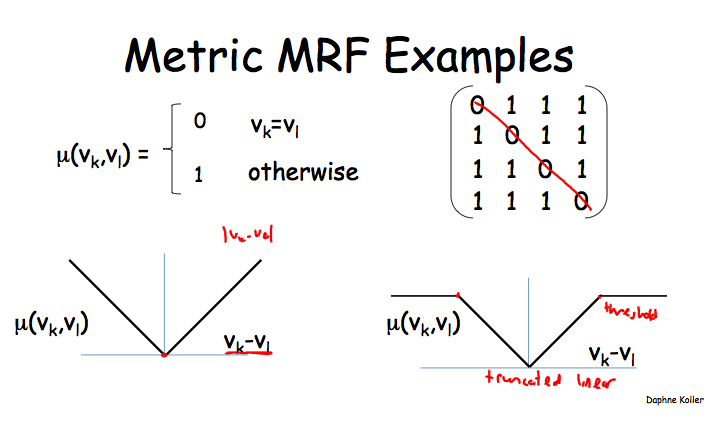
第一个定义就是说,只有当两个变量的取值相等时,距离为0,否则就为1;应用场景可以是image segmentation,它要求相邻的superpixel要共享同一个object label。
第二个定义就是取两个变量取值的差的绝对值,但是正如左下方的那图示意的一样,这个距离值可能是无界的,所以可以像右下角那样做一个truncate。对应的例子是图像除噪,假设有一幅有噪声的图像,其像素值表示为\(X_i\),我们希望得到的是除噪后的图像,其像素表示为\(Y_i\),约束条件是每个\(Y_i\)要与\(X_i\)接近,并且\(Y_i\)也要与它的邻像素值接近。如果采用未作truncate的metric函数,那么可能过于严苛,造成\(Y_i\)也要与它的邻像素值过于接近,而实际上这个局部特点并不是那么要严格遵守的,像物体边界上的像素值是有可能与其邻像素不一样的。这种应用场景下,truncate后的metric函数就更合适。
但是它相对于factor形式有什么优势呢?我的理解是,它可能更有利于adapt到某个特殊的领域,可以人工设计一些feature并很方便地将它们融入到模型中。
Shared Features in Log-Linear Models
回到刚才的Ising Model,当时就提了一下“\(f_{i, j}\)是说这个feature只会应用于\(X_i, X_j\)这两个变量上”,实际上这个feature可以不局限于仅仅是这两个特定的变量,可以是任何两个相邻的变量,同时这个feature对应的权重\(w_{ij}\)也是可以共享的。
\[-\sum_{i, j} w_{i, j} f_{i, j}(X_i, X_j) \to -\sum_{i, j} w f(X_i, X_j)\]
同样方式可以用到单词标注的问题上,对于任意的\(X_i, Y_i\)都可以定义通用的feature,而不必每一对变量都定义一个。Image Segmentation的例子也是如此。
因此,我们只需要为每个feature \(f_k\)定义一组scopes,表示为\(Scopes[f_k]\),然后就有\(w_k \sum_{D_k in Scopee[f_k]} f_k(D_k)\)。
总之,相同的参数和结构模板可以同一个MN中复用(同一句话中不同的word及对应的label),同时也可以在不同的MN中复用(不同的句子中)。
(END OF THIS SECTION)
[PGM] Section 4. Representation-Local Structure
Overview
对于一个条件概率分布\(P(Y|X_1,...,X_N)\),如果假设每个变量都可以取K个值,那么完全使用表格的形式(tabulor representation)来描述这个分布的话,需要有\(K^(N+1)\)行,即指数级。
幸运的是,变量之间往往存在一些其它的局部结构关系(local structure),使得我们不需要这么行就能描述,甚至很compact地描述出这个条件分布。例如,Deterministic CPD, Tree-structured CPD, Logistic CPD, Noisy OR, Linear Guassian,本section后半部会都会涉及到。
先给出几个概念
- General CPD: 任何一个满足归一化条件的函数\(\phi(X,Y_1,...,Y_k)\),都可以称为一个General CPD,即对所有的\(y_1,...,y_k\),\(\sum_x \phi(x,y_1,...,y_k)=1\)。
- 特定上下文独立(Context-Specific Indepedence):\(P \models X \perp_c Y | Z, c\),c可以是一些其它变量的具体取值。
Tree-Structured CPD
如下图所示,这是实际是\(P(J|L_1,L_2,C)\)的条件概率分布,如果没有局部结构的话,那么应该有\(2^3=8\)个概率分布,而图中只有4个概率分布产出,这就是局部结构将问题简化了。
Choice可以看作学生寄出了第一种推荐信还是第二种,Job表示工作申请是否被接收。这里实际上存在着一个上小节中的概念“Content-Specific Independence”,具体来说,就是\(P \models (L_1 \perp_c L_2 | J, c)\),例如学生只寄出了第一种推荐信,并且最后申请未成功,那么公司是否接收到了那封信的概率不会被公司是否接收到了第二种推荐信影响(因为第二封绝对没有寄出,公司以概率100%未收到这封信)。
这个Choice也称为Mulitplexer,它唯一地选择了一条路径。更一般地,
其中变量A就是multiplexer,是一个离散值,它的取值范围是1...K,而Y的取值以概率1等于\(Z_A\)。
Independence of Causal Influence
Noisy OR CPD
举例来说,引起咳嗽的原因可能有很多,可能是流感,普通感冒,过敏,甚至是偶然,这些原因对产生咳嗽这个结果是OR的关系。
图中每个\(Z_i\)表示\(X_i=1\)被触发的情况下,它本身是否成功产生了咳嗽。其可能性为\(P(Z_i=1|X_i)=\lambda_i\)。给定这个结构,那么最终产生咳嗽的可能性需要考虑所有这K个可能的因素,得到\(P(Y=1|X_1,...,X_k)\),计算方式如上图所示。
除了Noisy OR之外,还可以有Noisy AND/MAX等,只是计算\(P(Y=1)\)的方式不同。
Sigmoid CPD
由于sigmoid函数本身的值域就是0-1之间,所以其输出可以看作是一个概率值(实际是CRF,后面的章节有提到)。其它的地方也没啥新鲜的,只是通过线性模型从各个\(Z_i\)得到\(Z\),再输入到sigmoid函数里。当权重\(w\)的尺度被放大后,斜率变大,sigmoid的函数图像就会更sharp一些。
Continuous Variables
前面的Y都是离散变量(实际上都是0-1变量),下面的是连续型变量,像下面这个例子中,目标变量是S(传感器对温度的度量值),这是一个正态分布的连续变量,它在下一时刻结果依赖于外界温度O和室内温度T两个方面,并利用线性插值得到正态分布的期望值(线性高斯模型Linear Gaussian)。如果也考虑到是否开着门这个离散变量D,那么不同条件下正态分布的参数(插值参数,方差)是不同的,这样就变成了Conditional Linear Gaussian。
不废话了,直接上图
有线性高斯,也就必然可以有非线性的。课程中给了几个例子都没太懂,只是知道有这个么个非线性的东西应该就成了。
[PGM] Section 3. Representation-Template Models
Overview
模板模型实际就是在变量的基础上做了一层抽象,其中的一个模板变量可以实例化成N个实际的变量。
以血型为例,A的血型依赖于A的父母,而B的血型也依赖于B的父母,等等。而子女与父母之间的这种依赖关系以及之间参数(具体来说就是CPD)则是通用的,是可以在两个家族间共享的。同样的,A的后代的血型同样也是依赖于A及其配偶的血型,因此这种参数甚至还可以在同一个家族内共享。
类似的例子还有前面那个学生S,课程C和得分G的例子,不同的学生在不同的课程有不同的得分,但是他们之间共享S,C,G之间结构及其CPD参数。
模板变量:一个模板变量\(X(U_1, U_2, ..., U_k)\)可以实例化多次,即\(U_i = u_i\),如果血型的例子,则模板是Genotype(person),实例化后的变量则是Genotype(A), Geontype(B), ......
模板模型:这个东西就是描述实际变量如何从模型中继承依赖关系的一种语言。下面介绍的Dynamic Bayesian Networks就是描述时序模型的一个模板。
时序模型 Temporal Model
以X(t)表示随机变量X在时刻t的取值,对任意的t<=t',X(t:t')表示X(t)至X(t')的若干个变量,时序模板的目的就是要表示这一系列变量的联合概率分布P(X(t:t'))。
两个基本假设
- Markov Assumption: X(t)的取值依赖于之间一个时刻的X(t-1)的取值,而与其它时刻无关(独立);
- Time Invariance: 时间不变性,即\(X(t+1|t) = X(t+k+1|t+k) = X(t'|t)\)。
前面的两个假设不一定在所有场景下都是适用的,因此可以再扩展一下,X可以不止是一个随机变量,而是一个状态(state),而这个状态可以是若干个随机变量组成。例如,一个机器人在某时刻的位置为Loc(t),那么其下一个时刻的位置并不只依赖于这个Loc(t),还与当前进的方向,前进的速度等参数有关,因此可以抽象一下,以State(t)作为一个单位,表达这个时刻下各个因素的联合分布,而其下一个状态State(t+1)则完成依赖于这个State(t)。总结来说,就是redesign the model。
有了这两个简化的假设之后,后面就好办了,因为我们只需要给出一个初始状态,再给出一个从t到t+1的转移模型,这事儿就搞定了。
-
初始状态比较容易描述,实际就是把初始状态下各个变量之间的关系及具体的CPD参数用BN(0)表达。
-
转移模型可以使用2-time-slice Bayesian Network(2TBN)来描述。
2-time-slice Bayesian Network(2TBN)
定义于变量\(X_1, ..., X_N\)的转移模型2TBN是一个BN的片段,其中的结点包括\({X'}_1,...,{X'}_N\)以及\(X_1, ..., X_N\)的一个子集,且仅有前者有对应的父结点及CPD。它们联合表达了以下条件分布
\[P(X'|X) = \prod_i P({X'}_i|Parent({X'}_i))\]
带有初始状态的2TBN称为一个DBN。
Ground Network(Dynamic Bayesian Network)
对于一个时间序列0...T, 其对应的Ground Network的结构为
- \(X_1^{0},...X_n^{0}\)的模型为BN(0)
- \(X_1^{t},...X_n^{t}\)的模型为DBN
隐马尔科夫模型HMM
课程这里只简单介绍了下,没有深入细节,主要篇幅花在了语音识别的应用上。
HMM可以看作是BN的一个子类,但是它的变量之间的级别上几乎就没有复杂的结构关系,它主要的特点是在转移矩阵上的稀疏性和重复性,即它的复杂性体现在同一个变量在不同时刻取值的变化的转移概率分布。
HMM的主要应用领域包括语音识别,自然语言处理等。
模板模型Plate Model
正如overview里所述,模板模型的核心就是share across and within diferrent models。比如翻硬币的例子,每次的结果都是一个iid的随机变量,而它们的取值(正,反)分布是相同的。下图中,每一个outcome被使用t作为index表达是哪一次的toss的结果。
再复杂一点的模板,例如Nested Plates & Overlapped Plates,直接上图。
每个D使用c作为index,即每个课程有一个难度值,而I和G使用(c,s)作为index,也就是说每个学生上每门课都会有个分数,而每个学生上每门课时都有一个适合度(在这方面是否够聪明)。
如果认为学生的聪明程度不依赖于一门课程的话,那么上面的这个模型就不合适了,于是就有了Overlapped Plates
同一个模板下衍生出来的模型都是共享参数据,像这里的\(P(G|D,I)\)等等。后面还提了一个Collective Inference,就是用若干个衍生出的了模型来做全局的推演,没太懂,就不费话了。
最后正式给出Plate Dependency Model的定义
对于一个模板变量\(A(U_1, ..., U_K)\),其中\(U_i\)为index,它们若干个模板父变量\(B_1(PU_1),...,B_m(PU_m)\),其中每个\(PU_j\)都是\((U_1, ..., U_K)\)的一个子集(No indices in parent that are not in child),那么就可以定与其相关的一个CPD \(P(A|B_1,...,B_m)\)。
当把模板变量实例化为\((u_1, ..., u_K)\)之后,它就形成一个实例的网络。
关于前面的那个子集的约束,举例来说,假如G(c, s)表示一个学生在某门课上的得分,那么它不能作为这个学生整个评价的父结点(整体评价只与s相关,即Eval(s)),这需要集合所有c的G(c, s)才能形成一个有实际意义的CPD。
[PGM] Section 2. Representation-Bayesian Networks
Semantics and Factorization
直接上一个文中给出的例子,随机变量是课程难度D,学习智力I,课程成绩G,推荐信L,学生的SAT分数S(不知道具体是啥东西)。每个随机变量对应图中的一个结点。
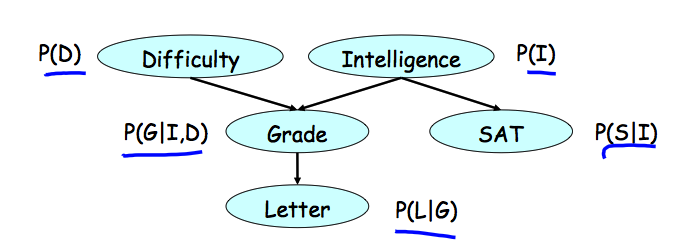
各个变量之间的依赖关系则由图中的箭头表示,每个结点与其所有父结点共同形成一个局部的条件概率分布,例如G的取值条件依赖于D和I的取值,而没有父结点的变量则只有一个边缘分布或者先验分布。
图中的结点和结点间的关系有效地表示了条件概率分布,而各变量的联合分布则可以通过这些条件概率分布(或者更一般地,因子)之间的乘积来表达。实际上,每个联合分布都可以写成chain rule的形式,而利用图中表达出的条件独立性进行简化,得到的就是各个条件概率分布的乘积。建议自己动手搞一下,更容易理解。
下面给出几个相关的定义
- Bayesian网络定义为一个有向无环图(DAG)G,每个结点表示一个随机变量\(X_1, ..., X_n\)。对于每个结点\(X_i\)都有一个对应的CPD(条件概率分布),表示为\(P(X_i|Par_G(X_i))\)。
- Bayesian网络通过链式规则表达一个联合概率分布\[ P(X_1, ..., X_n) = \Pi_i P(X_i|Par_G(X_i))\]
- 令G为一个关于\(X_1, ..., X_n\)的Bayesian网络,那么如果其联合概率分布P可以表达为上面的链式形式,那么就说P factorizes over G。(不知道怎么翻译,直接copy了)
Reasoning Patterns
- Causal Reasoning:由因及果(这里的因果用得都不准确,只是为了便于理解),例如,学生智力I越高,其得到推荐信L的概率越高,即\(P(l^1) < P(l^1|i^1)\)。顺向箭头的方向的影响。
- Evidential Reasoning:由果推因,例如,观察到学生的课程得分很低时,那么这门课难度高的可能性更大,即\( P(d^1) < P(d^1|g^3)\)。逆着箭头方向的影响。
- Intercausal Reasoning: 两个因之间的影响,例如,观察到得分很低时,学生智力可能较低,但如果同时观察到课程很难时,那么学生智力可能未必有那么低,即\( P(i^1|g^3) < P(i^1|g^3, d^1)\),如果再已经学生的SAT很高,那么课程难度可能就更高。再例,Z = X | Y,给定Z=1时,X和Y为1的概率都是2/3,但是如果给定了Y=1(Y explains away Z),那么X=1的概率就降为了1/2。
Flow of Probabilistic Influence
啥时候X可以影响到Y
| 方向 | 是否可以影响到 |
| X->Y | YES |
| X<-Y | YES |
| X->W->Y | YES |
| X<-W<-Y | YES |
| X<-W->Y | YES |
| X->W<-Y | NO |
简单来说,XY有因果关系时,或者同为果时可以影响到,而同为因时无法影响到。需要注意的是,这里的同为因的情况与前面Intercausal Reasoning中的例子不同,这里没有给定果W的取值。鉴于最后一种情况的特殊性,把X->W<-Y称为V结构(v-structure)。
活跃路径(Active Trails):一条路径\(X_1-X_2-...-X_n\)是活跃的,如果整条路径中不存在V结构,即\(X_(i-1) -> X_i <- X_(i+1)\)。
啥时候在给定Z的情况下X能影响到Y
| 方向 | W not in Z | W in Z |
| X->W->Y | YES | NO |
| X<-W<-Y | YES | NO |
| X<-W->Y | YES | NO |
| X->W<-Y | NO | YES |
这里面的最后一行可以跟上小节里的例子对应上了。
用最开始那个图给出一个例子,S-I-G-D这条路径,啥时候S能影响到Y?当给定Z时,或者啥都没给定时,S无法影响到D,而未给定I并且给定G的情况下时,S可以影响到D。
活跃路径(Active Trails):给定Z的情况下,一条路径\(X_1-X_2-...-X_n\)是活跃的,如果其满足以下两个条件
- 对于任何一个V结构\(X_(i-1) -> X_i <- X_(i+1)\),有\(X_i\)或者至少一个其后续存在于Z之中;
- 没有其它的变量位于Z之中。
Independencies
对于随机变量X和Y,定义独立性\(P \models X \perp Y\),如果满足
- \(P(X, Y) = P(X)P(Y)\)
- \(P(X|Y) = P(X) \)
- \(P(Y|X) = P(Y) \)
条件独立性,跟前面条件一样,只是每个term后面加了个|Z。不再详述了。
举个例子,硬币作为一个变量C,每次投出的结果作为变量\(X_i\),那么可知\(P \models X_1 \perp X_2\)不满足,但是\(P \models X_1 \perp X_2 | C\)。
条件性可能使用变量中的独立性失去,例如前面的例子,给定一个果后,两个因就不再相互独立了。
Bayesian Networks
d分离:如果在给定Z的条件下,G中不存在一条X-Y之间的活跃路径,那么就说X与Y是d分离的(d-spearated),记为\(d-sep_G(X, Y|Z)\)。
注意,d分离只是面向G的定义,与某个P没有直接关联。下面这个定理做了这件事:
定理:如果P factorize over G,并且满足\(d-sep_G(X, Y|Z)\),那么P满足\(X \perp Y | Z\)。证明过程使用了对不同变量分离\(\Sigma\)的方法,具体过程略。
换句话说,如果factorize成立,那么从G中读出的每一个d分离,P中都有一个条件独立性与之对应。例如,G中任一结点在给定父结点后,都与其子结点d分离,于是通过定理可知,如果factorize成立,那么P中任意一个变量都在给定父变量后,与其子变量相互独立。
收集所有G中的d分离,并通过定理可知:“G中所有的d分离的集合”必有一个“条件独立性集合”与之对应,这个由G引出的条件独立性集合定义为 \(I(G) = \{(X \perp Y| Z): d-sep_G(X \perp Y|Z)\}\)。注意,I(G)是G的函数,它只是定义一个条件独立性的集合,对于任意一个给定的P,它可能满足I(G),也可能不满足。而当P满足I(G)时,我们就说G是P的一个I-map。一个特殊的情况,I(G)为空集时,它是所有P的I-map。
Factorization => Indepenence
- 如果P factorize over G,那么G是P的一个I-map;
- 如果G是P的一个I-map,那么P factorize over G
需要注意的是,一般情况下,G中表现出的独立性未必是P中包括的所有的独立性,很可能只是一个子集,但是只要P能够满足I(G),那么G就是P的I-map,P就可以factorize over G,完全encode P中所有独立性的图并不是G。
至此,P与G之间关于独立性的关联已经建立起来。最后抄一段PPT中的总结:

Naive Bayes
朴素贝叶斯假设\(X_i \perp X_j | C\) for all \(X_i, X_j\),即在图模型的表示中每个\(X_i\)只与类变量\(C\)相关联,与不同\(X_i, X_j\)无关联。基于这个假设,可得联合概率分布为
\[P(C, X_1, ..., X_n) = P(C)\Pi_{i=1}^{n}P(X_i|C)\]
朴素贝叶斯分类器(假设只有两类),实际就是比较两个类的后验。
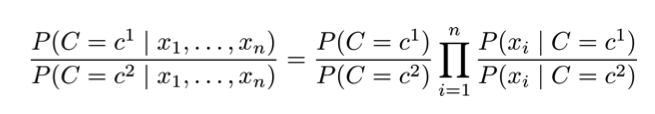
朴素贝叶斯分类器应用于文本数据
- Bernoulli朴素贝叶斯:每个\(X_i\)表示一个字典中的term,\(P(X_i = 1|C)\)表示这个term出现在这个类C中的可能性,归一化条件为\(P(X_i = 1|C) + P(X_i = 0| C) = 1\)。
- Multinomial朴素贝叶斯:每个\(X_i\)表示一个实际出现在文档中的一个位置,\(P(X_i = "cat"|C)\)表示该位置出现的词为cat的可能性,归一化条件为\(\sum_{i=1}^{n}P(X_i|C) = 1\),其中n为字典中词的个数。
朴素贝叶斯的优点是容易搞,容易算,feature间弱相关时很给力,但是当feature间有强相关时,表现得就不咋地了。
[PGM] Section 1. Introduction
注:Coursera的PGM是我在2012后半年跟的网上课程,当时课时很赶,天天在赶作业,没有做太详细的总结,学完之后觉得还是挺有信息量的,所以打算现在再复习一遍,顺便把知识总结一下。
Motivation and Overview
概率图模型英文全称为Probabilistic Graphical Model,先解释一下各自的含义,概念比较虚可以结合后面的具体内容来理解。
- Model: 即Declarative Representation,或者说一个框架结构。这个结构可从给定的训练数据中学习得到或者通过专家设计。框架中一般有若干个参数,使用不同的算法来做训练training(with and without complete data)可以得到模型参数的取值,而在此之后就可以用这个带有参数的模型做对其它样本点来做推演inference(可以是exact,也可以是approximate)。
- Probablistic:用于表示数据中的不确定性,例如不完整的样本,噪声以及无法被Model识别出来的知识等。概率论提供了表达不确定性的工具,例如多元变量的联合概率分布等。
- Graphical: 利用图像的形式表达随机变量之间的依赖关系,例如贝叶斯网络(有向图)或者马尔科夫网络(无向图),temporal,plate models。变量之间的这种依赖关系也可以看作一种约赖,从而可以大大降低Model中独立参数的数量。
Preliminaries: Distributions
一些简单的概念
- 联合概率分布:最简单地可以表示成表格的形式;多个变量之间可能存在的独立性
- 条件概率分布:对联合概率分布表格的reduction and normalization
- 边缘概率分布:通过求和消除掉某些随机变量
Preliminaries: Factors
因子\( \phi(X_1, ..., X_k) \)定义为一个函数 \( Val(X_1, X_k) -> R\),而这个因子的域scope为\( \{X_1, ..., X_k\} \)。
概率分布都可以看作是特殊的因子,而因子概念本身则更加一般,因为它不需要遵守sum-to-one规则。因子可以看作是构建和操控概率分布的基础。
因子的操作
- Factor Product: \( \phi(A,B,C) = \phi_1(A,B)*\phi_2(B,C) \)
- Factor Marginalization: \( \sum_C \phi(A,B,C) \)
- Factor Reduction: eliminate some table rows, leave the rest (unnormalized)