4. Parsing, CFG and PCFG
语法解析问题
语法解析问题是比词性标注更高层的问题, 它以一个完整的句子做为输入, 以一棵对应的语法解析树作为输出。语法解析树中不仅反应了各个单词的词性, 也反应出了各个词之间的关系,比如短语(动词短语,名词短语等)甚至句子中的主谓关系等。举个课程中的例子:
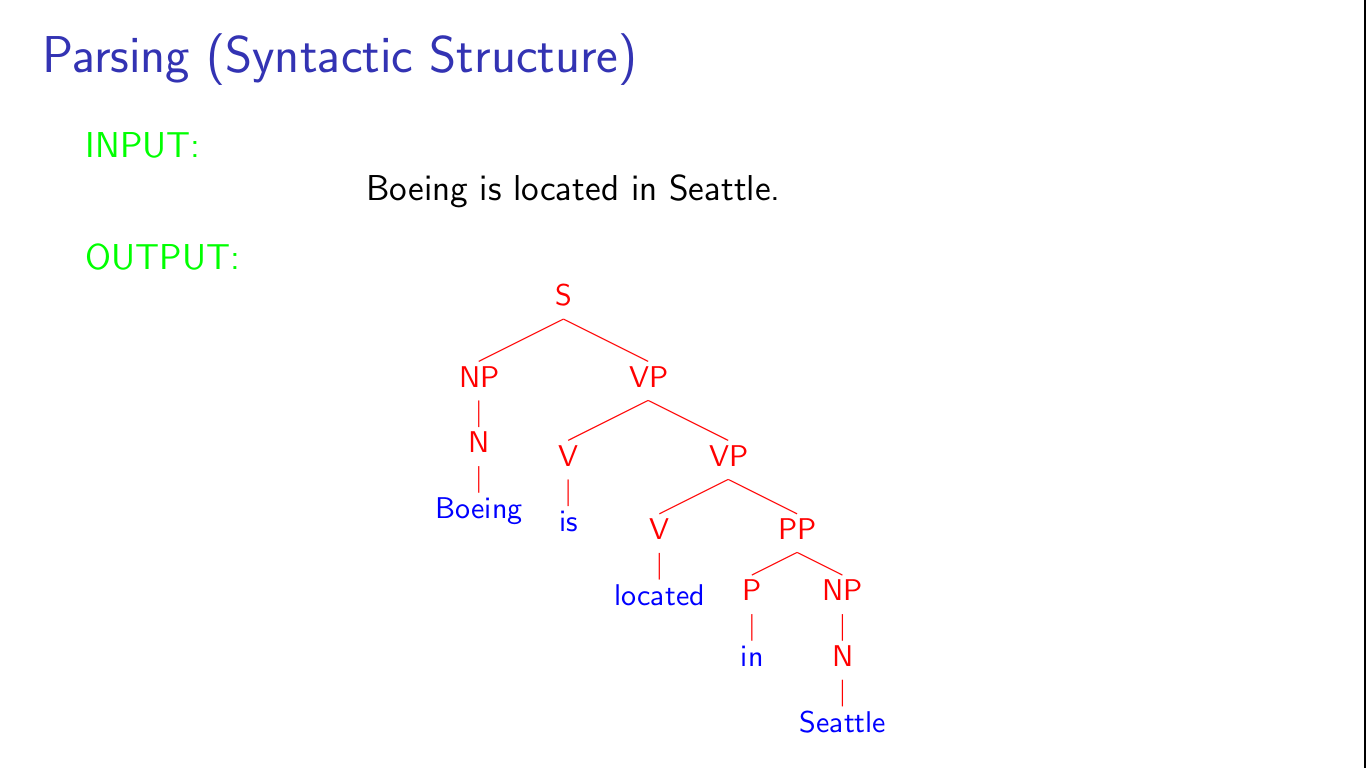
语法解析通常都会被表达成监督学习问题,而训练数据集可以是WSJ Treebank(for English);
语法树可以传达的信息:1. POS; 2. Phrase(VP, NP); 3. subject-verb;应用场景可以是机器翻译中,将源语言中单词间的顺序调换成目标语言中的词顺序。
上下文无关语法(Context-free grammer)
上下文无关语法对语言的一种形式化描述,具体表示为四元组\( G = (N, \Sigma, R, S) \),其中N表示非终结符,\(\Sigma\)表示终结符,S为特殊的开始符号,R则表示规则,即\(X \rightarrow Y_1 \dots Y_n, X \in N, Y_i \in (N+\Sigma), n \ge 0\)。例如:

最左推导:最左推导是一个序列\(s_1, ..., s_n\),序列的开头是\(s_1 = S\),其后的每一个元素\(s_i\)都是取前一个元素\(s_{i-1}\)中从左边数第一个非终结符,对其按照R中的某个规则进行展开而得到的结果,序列的结尾是一个全部由终结符构成的字符串,即\(s_n \in \Sigma^{*}\),例如,[S] [NP VP] [D N VP] [the N VP] [the man VP] [the man Vi] [the main sleeps]。
一个推导(derivation)实际就对应着一棵语法解析树,而推导最终的结果(终结符串)就是一个句子。一个CFG对应的所有推导结果的并集就是这个CFG所定义的语言;每个语言中的字符串有可能对应着不同的推导过程,因此一个句子可能对应着多棵语法树,这在一定程度上产生了歧义。比如,he drove down the street in the car这句话就可能有多种解析,in the car这个短语可以修饰drove形成动词短语,也可以修饰the street以形成名语短语,虽然第一种选择看起来更合理一些,但是CFG是无法区分出来的。
下面再给出几个可能出现的歧义情况
- POS歧义:her duck (NN, Vi)
- 介词短语所修饰的内容:比如前面提到的in the car
- 名词定语:the fast car mechanic (fast car -> mechanic, fast -> car mechanic)
PS: 这里本来还有一节是介绍英语语法的,这里先略过,后面如果有用到的话再说明。
概率上下文无法语法(Probabilistic Context-free grammer)
这个语法是为了解决上面提到的一个句子可能有多棵语法解析树的问题,这为每棵语法树赋予一个对应的概率值,而概率值最大的那个就被认为是这个句子的语法解析树。
实现上,它是对规则集R中的每条规则都赋予一个概率p,而一个推导实际就是从开始符S开始应用一系列规则最终生成非终结符串的过程,因此这个推导(或者说这棵对应的语法树)的概率就是在此过程中应用的所有规则概率的乘积,即
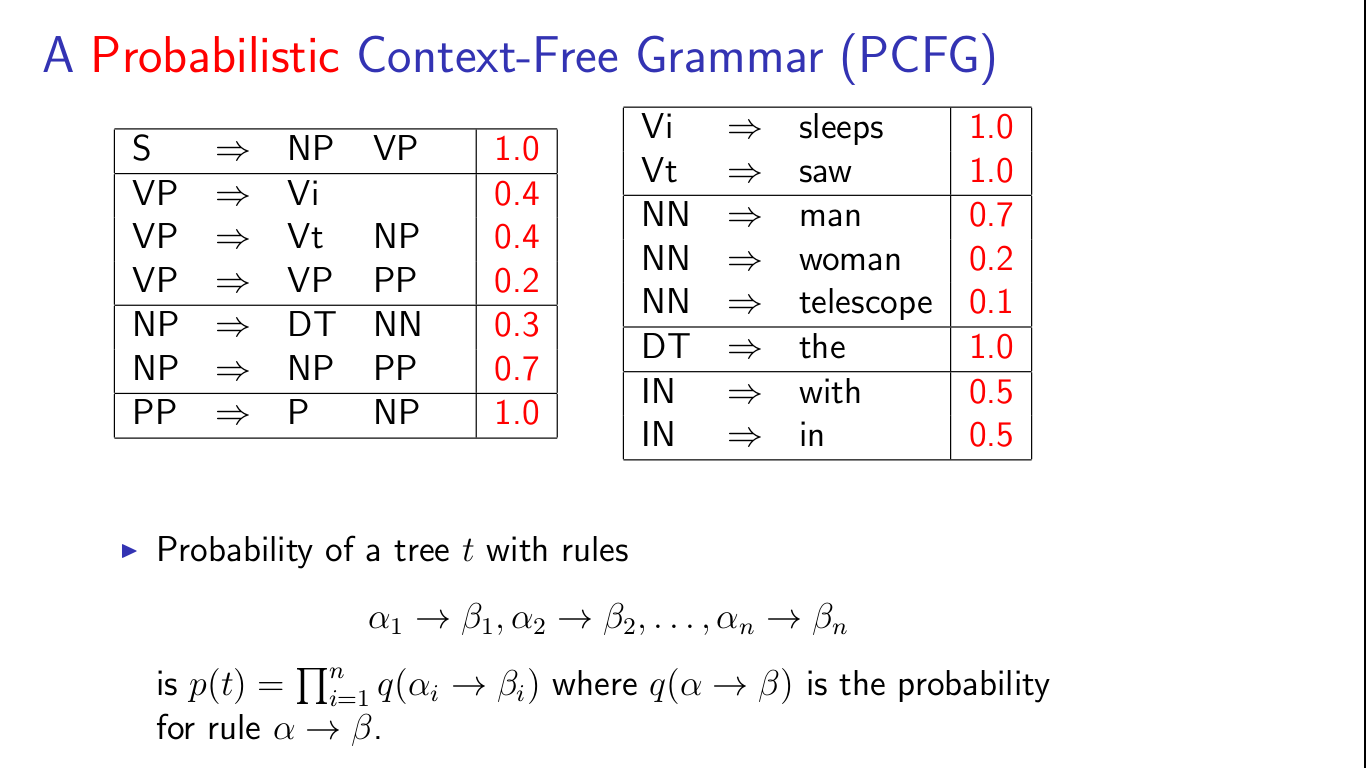
这个由部分概率(规则概率)到整体概率(语法树概率)的过程也是使用了独立性假设(与概率的链式规则做对比),即在推导的初始阶段应用的规则不依赖于后面应用到的规则,特别地,不依赖于最终的word。这也是后面提出lexicalized PCFG的动机。
当我们已经使用上面的方法为给定句子所对应的所有语法树都赋予了一个概率之后,下面要做的,就是取那个概率最大的语法树做为输出:
\[ opt\_tree = argmax_{t \in T(s)} p(t)\]
根据上面的流程,我们有两个问题需要解决:1. 如何为每个规则赋予一个概率值;2. 一个句子对应的可能的语法树是指数级别的,如何高效地为一个句子找到概率最大的语法树。
PCFG的参数估计
PCFG的参数就是每个规则的概率,当给定一个treebank之后,我们要做的实际跟N-gram类似:计数+MLE
\[ q_{ML}(\alpha \rightarrow \beta) = \frac{Count(\alpha \rightarrow \beta)}{Count(\alpha)}\]
如果训练数据确实是由PCFG生成的,那么当训练数据足够多时,MLE给出的结果将收敛于true PCFG。
PCFG解析
为了能多项式复杂度解决这个为给定句子找出最佳语法树的任务,还需要对PCFG加一些额外的约束,即要求语法G满足Chomsky Normal Form,简单来说就是要求四元组中的R只能取以下两种形式之一
- \(X \rightarrow Y_1 Y_2, X \in N, Y \in N\)
- \(X \rightarrow Y, X \in N, Y \in \Sigma\)
然后,使用一种称为CKY的算法来做这个解析工作,它的本质也是一种动态规划算法,如下

其中定义\(\pi (i, j, X)\)表示以非终结符X为root的覆盖word[i...j]的最佳语法树所对应的概率是多少。动态规划的过程是从长度最短的子句(单词,长度为1)开始,自底逐步向上,直至开始符S覆盖整个句子作为终结。每一步需要考虑覆盖的字句的长度以及对应的非终结符,计算复杂度为\(O(n^3N^3)\)。
3. Tagging Problem and Hidden Markov Model
标注问题
应用:词性标注,命名实体标注,命名实体抽取,中文分词等
目标:从训练数据中获取一个函数或者算法,使得它在接收一个句子作为输入时能产出一个标注序列。
约束:local(一般来说,单词can更可能是一个动词而不是名词),contextual(the后面的更可能是一个名词,而不是动词)
生成模型和判别模型
监督学习:给定一个训练集\((x_i, y_i), i = 1...n\),得到一个从y到x的映射关系\(f(x)\)。
判别模型:从训练集出发,获得一个条件概率分布\(p(y|x)\);对于任何一个测试样本x,定义\(f(x) = argmax_y p(y|x)\)。
生成模型:从训练集出发,获得一个联合概率分布\(p(x, y) = p(y)p(x|y)\)。
生成模型比判别模型拥有更多的信息,因为任何条件概率分布都可以由联合分布通过边缘化得到。
\[p(y|x) = \frac{p(y)p(x|y)}{p(x)} = \frac{p(y)p(x|y)}{\sum_y p(y)p(x|y)}\]
对于测试样本x,生成模型要做的跟判别模型本质上是一样的
\[f(x) = argmax_y p(y|x) = argmax_y p(y)p(x|y)\]
其中分母\(p(x)\)不影响argmax_y,所以可以被忽略掉。
隐马尔科夫模型HMM
基本定义
HMM是一种生成模型,对于任意一个单词序列\(x_1, ..., x_n\),任意一个标记序列\(y_1, ..., y_n\),HMM定义的是一个联合分布
\[p(x_1, ..., x_n, y_1, ..., y_n)\]
而当给定这个分布,同样再给出测试样本\(x_1, ..., x_n\)时,我们要做的就是找到能最大化联合分布的那一个\(y_1, ..., y_n\)
\[argmax_{y_1, ..., y_n} p(x_1, ..., x_n, y_1, ..., y_n)\]
跟第二章讲的一样,HMM为了简化计算都会有一个对上下文长度约束的假设。Trigram的假设是说
\[p(x_1, ..., x_n, y_1, ..., y_{n+1}) = \Pi_{i=1...n+1} q(y_i|y_{i-2}, y_{i-1}) \Pi_{i=1...n} e(x_i|y_i)\]
其中\(x_1, ..., x_n \in V, y_1, ..., y_n \in S, y_{n+1} = STOP, y_{-1} = y_0 = *\)。所以这个模型的参数就是
\[q(s|u, v), s \in S \cup \{STOP\}, u, v \in S \cup \{*\}\]
\[e(x|s), s \in S, x \in V\]
回过头来再看前面这个联合分布,等号右侧的第二项实际就是\(p(x|y)\),而第一项就是\(p(y)\),所以说HMM是生成模型。
参数估计
要想使用这个模型就得先把q和e这两套参数先从训练数据中搞出来:
对于q参数,可以直接借鉴上一章中language model里的smooth estimation方法,比如线性插值(就是带\(\lambda\)的那套方法);
对于e参数,最直接的方法就是MLE,然后我们又遇到了同样的问题:Sparse Data,肿么办?
课程中给出了一个word class的方法:简单来说就是高频词直接MLE(比如出现次数大于等于5的),低频词则按照一定的特征划分到有限个类别中,类别可以是twoDigitNum, containDigitAndSlash, allCaps等,通常需要人工指定规则,划分之后针对\(e(wordClass|y)\)来做统计,而不是原来的\(e(word|y)\),以丢失word中一些信息为代价来保证有估计得到的参数足够的统计意义。
Viterbi算法
假设使用前面的方法已经获得了想要的参数,那么HMM就已经构造完成了,后面就是看怎么用这个模型来对测试样本做标注了,即
\[argmax_{y_1, ..., y_{n+1}} p(x_1, ..., x_n, y_1, ..., y_n)\]
其中\(y_{n+1} = STOP, y_{-1} = y_0 = *\)。首先说暴力方法是行不通的,因为需要\(O(|S|^{n})\),指数级别,会被搞死的。。。
下面要说Viterbi算法就是利用动态规划的思想来解决这个标注问题的,懒得费劲了直接上图。

其中递归式\(\pi(k, u, v)\)表示的是"maximum probability of a tag sequence ending in tags u, v at position k",bp里面存在是回溯指针,用于循环结束后向回寻找最优的tag sequence。
由于Viterbi算法计算每个\(\pi(k, u, v)\)项需要遍历所有\(S_{k-2}\),而一共有n*|S|*|S|个项需要计算,所以其算法复杂度为\(O(n|S|^3)\),比指数级别的暴力搜索要强很多。
这个算法的优点是简单,而且在一些应用中也表现得很好,缺点就是前面所说的e参数不好估计。
PS:这个课程里讲的HMM其实并不全面,HMM相关的有三类问题
- 给定模型,它能产出给定x序列的可能性是多大(forward算法)
- 给定模型,给定x序列所对应的最可能的y序列是啥(这个就是课程里讲的标注问题,Viterbi算法)
- 非监督条件下如何估计参数,即训练数据中没有y的情况下怎么搞(forward-backward算法,本质是EM)
52nlp网站中有一系列很赞的文章《HMM学习最佳范例》,里面讲得更加细致全面一些,所以把相关的链接放在这里,就当是备忘吧。
2. Language Modeling Problem
语言模型问题的定义
词汇表:\(V \) = {the, man, telescope, ...}
语句:\(V^{+}\),无限多个,由词汇表中的若干个词加上结尾处的STOP标记组成;例如,the fan saw Beckham STOP,甚至the the the STOP也属于这其中。
输入:训练样本,各种各样实际中使用的句子,可以从报纸来,也可以从网页来。
输出:一个面向语句的概率分布,满足以下条件;实际表达的意义就是让像人话的句子概率更高,反之则更低。
\[ p(x) >= 0, \sum_{x \in V^{+}} p(x) = 1\]
这个模型有啥用
原始的出发点是语音识别,因为一段语音通常可以被识别成不同的句子,例如,recognize speech vs wrench a nice beach,但是前者明显更像人话,这时应用语言模型就可以辨识出这段话是前者的可能性更大。
另外,语言模型中的估计方法(estimation/smoothing method)也会很广泛地应用到NLP的其它问题之中,这也算是一个用途吧。
一个简单的方法
想解决语言模型问题,实际就是想得到一个合适的\(p(x)\),如何做呢?一个简单的方法就是记数,假设训练样本的规模是N,统计下训练样本中每个x出现的次数,然后\( p(x) = C(x) / N\)。但是这样做的问题是,如果有一个训练样本中从未出现的句子,那么它的概率就是0了,也就是说这个未出现的句子无论具体内容是啥,\( p(x)\)都认为它不是人话。
马尔科夫模型
马尔科夫模型假设第n个词出现的可能性只依赖于它的前k个词,即第n-1至第n-k个词。由于后面要讲是三元模型,所以这里用的是就三阶马尔科夫模型。具体来说,
\[p(x_1, ..., x_n) = p(x_1)*p(x_2|x_1)*p(x_3|x_1, x_2)*...*p(x_n|x_1, ..., x_{n-1})\]
这个是没有加入马尔科夫的链式规则,精确的等式,但是如果我们想用这个来算语言模型的话,就得从训练数据中估计出每个\(p(x_i|x_1, x_2, ..., x_{i-1}) \),这样我们就需要估计出\(O(|V|^{n})\)个参数。参数太多显然是没法搞的,因为参数越多,需要的训练数据就越多,否则就是造成参数极不稳定,甚至没什么意义。
如果加入前面提到的三阶马尔科夫假设的话,问题就简化了
\[p(x_1, ..., x_n) = p(x_1)*p(x_2|x_1)*p(x_3|x_1, x_2)*...*p(x_n|x_{n-2}, x_{n-1})\]
这样参数的个数就降到了\(O(|V|^3)\)(其实这个量级仍然太大,后面会讲到解决方法)。如果我们假设\(x_{-1} = x_0 = *\),表示开始符号,那么就可以将上式写成
\[p(x_1, ..., x_n) = \Pi_{i=1...n} p(x_i|x_{i-2}, x_{i-1})\]
还有个问题,就是上式只能表示长度为n的句子,而我们想要的是对任意长度的任意句子都有效的分布p。实际上,融合我们前面的定义\(x_n = STOP\),我们已经可以表示任意的句子了。
三元语法模型
把前面的三阶马尔科夫模型直接应用,就是三元语法模型,它包括以下两个部分
- 一个有限的词汇表\(V\)
- 对每个\(w \in V \cup {STOP}, u, v \in V \cup {*}\),都有一个参数\(q(w|u, v)\)
于是对任何一个句子\(x_1, ..., x_n\),其中\(x_1, ..., x_{n-1} \in V, x_n = STOP\),都可以直接它所对应的概率
\[p(x_1, ..., x_n) = \Pi_{i=1,...,n} q(x_i|x_{i-2}, x_{i-1})\]
举个例子,
\[p(the dog barks STOP) = q(the|*, *) * q(dog|*, the) * q(barks|the, dog) * q(STOP|dog barks)\]
好了,到这里,剩下的最后一个问题就是参数\(q(w|u, v)\)怎么从训练数据中估计出来了,最简单的方式就是MLE(极大似然估计法),即
\[q(x_i|x_{i-2}, x_{i-1}) = \frac{Count(x_{i-2}, x_{i-1}, x_i)}{Count(x_{i-2}, x_{i-1})}\]
正如前面所述的,这里参数的个数是\(O(|V|^3)\),依然不少,要使用这种方法得到稳定的参数估计值就需要使用大量的数据。否则的话,上式的分子分母都极有可能是零,那么得到的参数意义就不大了。
使用Perplexity对模型进行评估
假设我们除了有用于训练模型参数的训练数据之外,还有一些测试数据,表示为\(s_1, s_2, ..., s_m\),那么就可以用这些测试数据来评估训练得到的模型的可用性。这里定义了perplexity这个概念,本质上就是模型对这些测试数据的对数似然性:
\[Perplexity = 2^{-l}, where l = \frac{1}{M} \sum_{i=1...m} log p(s_i)\]
其中M表示测试数据是总的单词数据,因此l代表的就是模型对单个词的似然性;测试数据与模型的适应程度越好,似然性越大,perplexity就越小。
下面是对几个模型的比较
- 均匀分布:\(q(w|u, v) = \frac{1}{|V|+1}\),无论上下文是啥,也不管当前词是啥,这个概率值总是固定的,这是一个很粗的模型,所以perplexity也很高为\(|V|+1\);
- 一元语法模型:也就是unigram,就是在训练数据上记数,完全不管上下文,在Goodman的实验中(|V|=50000),它的perplexity为955;
- 二元语法模型:就是只考虑前一个单词对当前词的影响,同一个实验中perplexity为137;
- 三元语法模型:就是前面花大篇幅讲的那个模型,考虑当前词前面两个单的影响,perplexity为74;这已经是足够好的效果了。
但是三元语法模型也有它的不足,它无法捕获长距离的依赖关系,但是考虑的上下文太多了,就又会出现sparse data的问题,使参数估计很困难。其实这里也就是一个bias-variance tradeoff,上下文考虑得多,自然bias就小,但是由于训练数据相对不足,variance就大了;相反地,如果上下文考虑得少,variance小,但是bias就大了,所以不得不做一些折衷, 讲师说trigram的方法就是一个比较好的折衷。
参数平滑方法
我觉得下面这些内容才是这段课程的重点,就是怎样解决前面提到的由于数据稀疏问题而造成的MLE估计不可靠的问题。课程里介绍了两个方法,一种是线性插值,另一种是katz-backoff的类递归方法。实际上还有很多其它的方法,可以参考Foundations of Statistical Natural Language Processing中的第6章,也许未来这章的内容我也会总结一下写在blog上。
线性插值
这个方法的动机就是上一小节最后提到的bias-variance trade-off,既然unigram的variance小,而trigram的bias小,为啥不想个办法整合一下呢?于是就有了
\[q(w_i|w_{i-1}, w_{i-2}) = \lambda_1 \dot q_{ML}(w_i|w_{i-1}, w_{i-2}) + \lambda_2 \dot q_{ML}(w_i|w_{i-1}) + \lambda_3 q_{ML}(w_i)\]
\[\lambda_1 + \lambda_2 + \lambda_3 = 1, \lambda_i >=0\]
容易证明这个线性插值所产生的\(q(w_i|w_{i-1}, w_{i-2})\)也是一个合法的概率分布,符合归一化及>=0的条件。
各个\(q_{ML}\)都可以从训练数据中直接计算得到,那么剩下的事就是如何计算\(\lambda_i\)了。这里使用的方法是搞一份validation data,记这份数据中各个三词序列出现次数为\(c'(w_1, w_2, w_3)\),那么log-likelihood的表达式即为
\[L(\lambda_1, \lambda_2, \lambda_3) = \sum_{w_1, w_2, w_3} c'(w_1, w_2, w_3)logq(w_3|w_1, w_2)\]
表达式中未知参数只有\(\lambda_i\),所以使用这个表达式对其求偏导应该就可以了。另外,前面提到的perplexity实际就是log-likelihood的变形,所以这种方法就也是在寻找一组参数,使perplexity最大化。
再进一步,前面这种方式得到是一个不依赖于具体\(w_1, w_2\)的\(\lambda_i\)。极端情况下,如果我们已知\(w_1, w_2\)出现的次数足够多,还不如直接用trigram就好了(\(\lambda_3 = 1\),其它两个为0),相反地如果\(w_1, w_2\)出现极少,那么\(\lambda_1\)就应该相应的更重一些。总结一下就是说,最好是能让\(\lambda_i\)能随着具体\(w_1, w_2\)出现的次数而变化。于是就出现了下面\(\Pi(w_{i-2}, w_{i-1})\)这个东西
\[C(w_{i-2}, w_{i-1}) = 0, \Pi(w_{i-2}, w_{i-1}) = 1\]
\[1 <= C(w_{i-2}, w_{i-1}) <= 2, \Pi(w_{i-2}, w_{i-1}) = 2\]
\[3 <= C(w_{i-2}, w_{i-1}) <= 5, \Pi(w_{i-2}, w_{i-1}) = 3\]
\[C(w_{i-2}, w_{i-1}) >= 5, \Pi(w_{i-2}, w_{i-1}) = 4\]
再然后就是依赖于\(\Pi(w_{i-2}, w_{i-1})\)的\(q\)
\[q(w_i|w_{i-1}, w_{i-2}) = \lambda^{\Pi(w_{i-2}, w_{i-1})}_1 q_{ML}(w_i|w_{i-1}, w_{i-2}) + \lambda^{\Pi(w_{i-2}, w_{i-1})}_2 q_{ML}(w_i|w_{i-1}) + \lambda^{\Pi(w_{i-2}, w_{i-1})}_3 q_{ML}(w_i)\]
实际上就是按照每个\(w_i\)的context出现的次数,即\(C(w_{i-2}, w_{i-1})\),来对\(w_i\)分组,每组使用一套\(\lambda\)参数。
Katz Back-off Model
这种方法的动机的是从训练数据里得到的ML估计是对存于在训练数据里的词的过高估计(尤其是对仅出现一次的词),而对未登陆词的过低估计(ML估计都是0),所以需要从已有词的概率中抽取出一部分,分给这些未登陆词。以bigram为例,已存在词的次数被折掉了一部分(0.5这个数是个经验值,也可以使用前面的validation set方法来估计出来),
\(Count^{*}(w_{i-1}, x) = Count(w_{i-1}, x) - 0.5\)
而折掉的概率一共是
\[\alpha(w_{i-1}) = 1 - \sum_{w} \frac{Count^{*}(w_{i-1}, w)}{Count(w_{i-1})}\]
这些概率会根据unigram中各个x的概率比例再重新分配。具体如下:定义两个集合,\(A(w_{i-1}) = \{w: Count(w_{i-1}, w) > 0\}, B(w_{i-1}) = \{w: Count(w_{i-1}, w) = 0\}\),则有
\[q_{BO}(w_i|w_{i-1}) = Count^{*}(w_{i-1}, w_i) / Count(w_{i-1}), w_i \in A(w_{i-1})\]
\[q_{BO}(w_i|w_{i-1}) = \alpha(w_{i-1}) \frac {q_{ML}(w_i)} {\sum_{B}q_{ML}{w_j}}, w_i \in B(w_{i-1})\]
也就是说如果\(w_i\)出现在了训练语料中就使用高阶模型,否则的话就回退到低阶的模型中,在bias和variance中取一个折衷。基于上面bigram的定义,可以继续定义trigram模型,使未登陆词回退到bigram中。
最后是说可能对trigram模型的进一步改进方法,包括topic model,语法模型等,但是"It's generally hard to improve on trigram models though!!"
1. Introduction to NLP
之前在Coursera上找到了一门NLP的课,也跟过一段时间,但是没跟完。。。本来想再开课时再跟一次,但是从网站上看貌似是短期内不会重开了,好在教学视频都在,只好自学一下了,顺便把笔记记在这里。
第一周的课分成了三个部分,这里是第一部分,对NLP的简单介绍,由于不涉及具体的NLP算法,所以我也只是简单带过了。
什么是自然语言处理
- NLU:自然语言理解,把languge作为computer的输入,让后者理解输入的是啥;
- NLG:自然语言生成,把language作为computer的输出,即让后者生成自然语言;个人感觉这应该是在NLU的基础上才能做的。
具体应用的举例
- 机器翻译:理解源语言,生成目标语言,这个应该是NLU+NLG。
- 信息抽取:从一段非结构化的自然语言的文本中抽取出关键信息,如这段话描述的时间,位置,事件等结构化信息(这些结构后信息通常存于db中),换句话说就是想把一段文本对应到一条数据库记录上。应该场景可以是复杂的search query或者statistical query。
- 摘要:同样也是NLU+NLG。需要先理解这段文本的意思,然后进行压缩,输出摘要内容。
- 对话系统:接受自然语言的问题,理解之,再做出回答,也是NLU+NLG。
基础的NLP问题:这些问题是解决上面具体应用的基石
- Tagging:标注问题,把一段文本做为输入,为每个单位打上一个标记,输出对应的标记序列。包括POS Tagging(词性标注),Named Entity Recognition(命名实体识别)。
- Parseing:解析问题,以一句话做为输入,辨识出它的语法结构,输出是一棵语法树。这两个问题后面都有章节具体地讲。
为什么NLP是个难题
一句话可能有各种层次上的歧义,包括acoustic level(like your vs lie cured),syntactic level(不同的语法树,从而造成不同的意义),semantic level(一词多义), discourse level(指代不明)。
课程包含的内容
- NLP问题:POS tagging,parsing,词义消歧
- 机器学习技术:PCFG,HMM,EM,log-linear model,estimation/smoothing techniques
- 应用:信息抽取,机器翻译等