[PGM] Section 2. Representation-Bayesian Networks
Semantics and Factorization
直接上一个文中给出的例子,随机变量是课程难度D,学习智力I,课程成绩G,推荐信L,学生的SAT分数S(不知道具体是啥东西)。每个随机变量对应图中的一个结点。
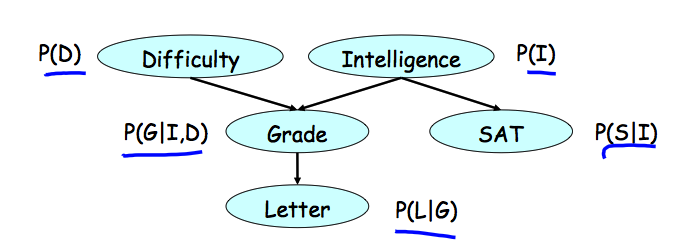
各个变量之间的依赖关系则由图中的箭头表示,每个结点与其所有父结点共同形成一个局部的条件概率分布,例如G的取值条件依赖于D和I的取值,而没有父结点的变量则只有一个边缘分布或者先验分布。
图中的结点和结点间的关系有效地表示了条件概率分布,而各变量的联合分布则可以通过这些条件概率分布(或者更一般地,因子)之间的乘积来表达。实际上,每个联合分布都可以写成chain rule的形式,而利用图中表达出的条件独立性进行简化,得到的就是各个条件概率分布的乘积。建议自己动手搞一下,更容易理解。
下面给出几个相关的定义
- Bayesian网络定义为一个有向无环图(DAG)G,每个结点表示一个随机变量\(X_1, ..., X_n\)。对于每个结点\(X_i\)都有一个对应的CPD(条件概率分布),表示为\(P(X_i|Par_G(X_i))\)。
- Bayesian网络通过链式规则表达一个联合概率分布\[ P(X_1, ..., X_n) = \Pi_i P(X_i|Par_G(X_i))\]
- 令G为一个关于\(X_1, ..., X_n\)的Bayesian网络,那么如果其联合概率分布P可以表达为上面的链式形式,那么就说P factorizes over G。(不知道怎么翻译,直接copy了)
Reasoning Patterns
- Causal Reasoning:由因及果(这里的因果用得都不准确,只是为了便于理解),例如,学生智力I越高,其得到推荐信L的概率越高,即\(P(l^1) < P(l^1|i^1)\)。顺向箭头的方向的影响。
- Evidential Reasoning:由果推因,例如,观察到学生的课程得分很低时,那么这门课难度高的可能性更大,即\( P(d^1) < P(d^1|g^3)\)。逆着箭头方向的影响。
- Intercausal Reasoning: 两个因之间的影响,例如,观察到得分很低时,学生智力可能较低,但如果同时观察到课程很难时,那么学生智力可能未必有那么低,即\( P(i^1|g^3) < P(i^1|g^3, d^1)\),如果再已经学生的SAT很高,那么课程难度可能就更高。再例,Z = X | Y,给定Z=1时,X和Y为1的概率都是2/3,但是如果给定了Y=1(Y explains away Z),那么X=1的概率就降为了1/2。
Flow of Probabilistic Influence
啥时候X可以影响到Y
| 方向 | 是否可以影响到 |
| X->Y | YES |
| X<-Y | YES |
| X->W->Y | YES |
| X<-W<-Y | YES |
| X<-W->Y | YES |
| X->W<-Y | NO |
简单来说,XY有因果关系时,或者同为果时可以影响到,而同为因时无法影响到。需要注意的是,这里的同为因的情况与前面Intercausal Reasoning中的例子不同,这里没有给定果W的取值。鉴于最后一种情况的特殊性,把X->W<-Y称为V结构(v-structure)。
活跃路径(Active Trails):一条路径\(X_1-X_2-...-X_n\)是活跃的,如果整条路径中不存在V结构,即\(X_(i-1) -> X_i <- X_(i+1)\)。
啥时候在给定Z的情况下X能影响到Y
| 方向 | W not in Z | W in Z |
| X->W->Y | YES | NO |
| X<-W<-Y | YES | NO |
| X<-W->Y | YES | NO |
| X->W<-Y | NO | YES |
这里面的最后一行可以跟上小节里的例子对应上了。
用最开始那个图给出一个例子,S-I-G-D这条路径,啥时候S能影响到Y?当给定Z时,或者啥都没给定时,S无法影响到D,而未给定I并且给定G的情况下时,S可以影响到D。
活跃路径(Active Trails):给定Z的情况下,一条路径\(X_1-X_2-...-X_n\)是活跃的,如果其满足以下两个条件
- 对于任何一个V结构\(X_(i-1) -> X_i <- X_(i+1)\),有\(X_i\)或者至少一个其后续存在于Z之中;
- 没有其它的变量位于Z之中。
Independencies
对于随机变量X和Y,定义独立性\(P \models X \perp Y\),如果满足
- \(P(X, Y) = P(X)P(Y)\)
- \(P(X|Y) = P(X) \)
- \(P(Y|X) = P(Y) \)
条件独立性,跟前面条件一样,只是每个term后面加了个|Z。不再详述了。
举个例子,硬币作为一个变量C,每次投出的结果作为变量\(X_i\),那么可知\(P \models X_1 \perp X_2\)不满足,但是\(P \models X_1 \perp X_2 | C\)。
条件性可能使用变量中的独立性失去,例如前面的例子,给定一个果后,两个因就不再相互独立了。
Bayesian Networks
d分离:如果在给定Z的条件下,G中不存在一条X-Y之间的活跃路径,那么就说X与Y是d分离的(d-spearated),记为\(d-sep_G(X, Y|Z)\)。
注意,d分离只是面向G的定义,与某个P没有直接关联。下面这个定理做了这件事:
定理:如果P factorize over G,并且满足\(d-sep_G(X, Y|Z)\),那么P满足\(X \perp Y | Z\)。证明过程使用了对不同变量分离\(\Sigma\)的方法,具体过程略。
换句话说,如果factorize成立,那么从G中读出的每一个d分离,P中都有一个条件独立性与之对应。例如,G中任一结点在给定父结点后,都与其子结点d分离,于是通过定理可知,如果factorize成立,那么P中任意一个变量都在给定父变量后,与其子变量相互独立。
收集所有G中的d分离,并通过定理可知:“G中所有的d分离的集合”必有一个“条件独立性集合”与之对应,这个由G引出的条件独立性集合定义为 \(I(G) = \{(X \perp Y| Z): d-sep_G(X \perp Y|Z)\}\)。注意,I(G)是G的函数,它只是定义一个条件独立性的集合,对于任意一个给定的P,它可能满足I(G),也可能不满足。而当P满足I(G)时,我们就说G是P的一个I-map。一个特殊的情况,I(G)为空集时,它是所有P的I-map。
Factorization => Indepenence
- 如果P factorize over G,那么G是P的一个I-map;
- 如果G是P的一个I-map,那么P factorize over G
需要注意的是,一般情况下,G中表现出的独立性未必是P中包括的所有的独立性,很可能只是一个子集,但是只要P能够满足I(G),那么G就是P的I-map,P就可以factorize over G,完全encode P中所有独立性的图并不是G。
至此,P与G之间关于独立性的关联已经建立起来。最后抄一段PPT中的总结:

Naive Bayes
朴素贝叶斯假设\(X_i \perp X_j | C\) for all \(X_i, X_j\),即在图模型的表示中每个\(X_i\)只与类变量\(C\)相关联,与不同\(X_i, X_j\)无关联。基于这个假设,可得联合概率分布为
\[P(C, X_1, ..., X_n) = P(C)\Pi_{i=1}^{n}P(X_i|C)\]
朴素贝叶斯分类器(假设只有两类),实际就是比较两个类的后验。
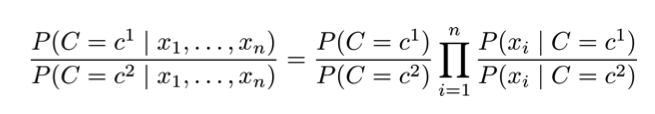
朴素贝叶斯分类器应用于文本数据
- Bernoulli朴素贝叶斯:每个\(X_i\)表示一个字典中的term,\(P(X_i = 1|C)\)表示这个term出现在这个类C中的可能性,归一化条件为\(P(X_i = 1|C) + P(X_i = 0| C) = 1\)。
- Multinomial朴素贝叶斯:每个\(X_i\)表示一个实际出现在文档中的一个位置,\(P(X_i = "cat"|C)\)表示该位置出现的词为cat的可能性,归一化条件为\(\sum_{i=1}^{n}P(X_i|C) = 1\),其中n为字典中词的个数。
朴素贝叶斯的优点是容易搞,容易算,feature间弱相关时很给力,但是当feature间有强相关时,表现得就不咋地了。
2023年2月14日 18:37
12th Class Time Table 2024 on this page. The Students Board are very curious to check Board of Intermediate Revised Exam Date 2024 for Arts Commerce and Science. Recently, the Intermediate Board has issued the 12th Date Sheet 2024 on the official website. +2 Date Sheet 2024 So those Students who are going to appear in the Inter Examination can download Time Table 2024 on the main portal.
2023年7月13日 23:10
Truecaller est simplement une application qui vérifie qui vous contacte. Ce type d’identification de l’appelant est important pour détecter les télévendeurs, les appels indésirables et les escrocs. truecaller recherche par numéro en ligne Truecaller classe les appelants comme Spam ou Safe en fonction des informations de contact des fournisseurs de réseau et des données des autres utilisateurs.
2023年7月14日 15:30
Assam 6th Class Syllabus 2024 will help Students to Prepare for pass Marks in All Exams the All Subjects, Assam Students to get a Clear idea of the Topics and Subtopics and According to it they can Decide on which topic to Focus more, Assam 6th Exam Conducted Every Year Month of March and April Months, This 6th Date Sheet 2024 Available at Official Website.as it helps Students to Plan their Preparations Assam 6th Class Syllabus 2024 Accordingly to Meet their Expectations, we Provide Students with All the Necessary Support and Allow them to Prove their Talent by performing best in their examination, The Students skill Profile Should move From being Predominantly Receptive to Productive.