Pairwise Markov Networks

前面的讲的Bayesian Network是有向图，这节说的Markov Networks是无向图。从最简单的pairwise的case说起。

有向图的局部结构所表达的意义很明确，比如从A到B的结构，表示的就是\(P(B|A)\)，而无向图则因为没有方向的概念，它就没有直接且有意义的概率分布来表示，所以只好用factor的概念来做抽象描述。

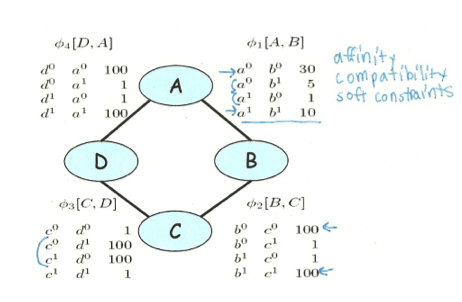
（我发现我越来越懒了，各种截图）

上面是一个例子，每个变量取值非零即一，而每条边上对应的factor，比如\(\phi (A,B)\)就表示这两个变量在各种取值下的权重，这里A和B取值相等时权重更高，表示这两个变量是比较正相关的。但是需要注意的是，每个factor都只是一个局部信息，它不会直接对应到我们最终得到的联合概率分布，甚到不能直接对应到与这两个变量相关的边缘分布或者条件分布上。这一点与Bayesian Network非常不同，用后面的例子一看就清晰了。

在有了这些factors之后，我们想要算这些变量的联合分布，做法就是直接利用factor product（如下），然后normalize一下就哦了。

\[ P(A,B,C,D) = \phi_1(A,B) * \phi_2(B,C) * \phi_3(C,D) * \phi_4(A,D)\]

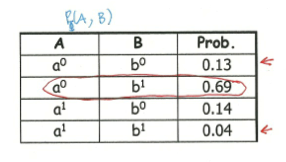
有了联合分布，自然可以算出一个边缘分布来，上面这个表格就是计算出来的\(P(A,B)\)，对比一下包含局部信息的\(\phi(A,B)\)，可以发现两者有天壤之别。原因就在于前面关于A和B的整体信息（实际上是受了C，D之间强烈取值不一致权重高的影响），而后者只是局部信息。

下面就是Pairwise Markov Networks的定义：一个包含结点\(X_1,...,X_n\)和边\(X_i, X_j\)的无向图，每条边上都有一个\(\phi_{ij}(X_i, X_j)\)，这个东西就是Pairwise Markov Networks。这里的Pairwise体现在，每个factor的domain只有两个变量。

General Gibbs Distribution

书接上回，前面提到了Pairwise的case中，每个factor中只涉及两个变量，它的表达能力足够了吗？我们考虑一个fully connected的pairwise MN，即任意两个变量之间都有一个factor，假设共有N个变量，且每个变量可以有d个取值，那么这些factor的product可以产生的组合数就是\(O(n^2d^2)\)，而实际上这N变量的联合概率分布应该是有\(O(d^n)\)个组合，二者之间还有有很大差距，这说明pairwise MN的表达能力并不足够。

为解决这个问题，就有人提出了Gibbs Distribution的概念，即定义一些General Factor \(\phi_i(D)\)，其中每个D可能包含一个或者多个变量（而不是pairwise中的2个变量），把这些factors集中在一起表示为\(\Phi = {\phi_i(D_i)}\)，后面的就都一样了，factor product+normalization，不费话了。所以实际上Gibbs Distribution所做的就是对每个factor的domain中的变量个数扩展到了任意个，同样的问题，这样表达能力就足够了吗？必须的，因为定义一个包含所有变量的factor都是可行的。

但是这种一个factor中有多个变量的形式，如何对应到Markov Network上呢，这个图咋画呢？结论就是Induced Markov Network，即当存在一个\(\phi_m \in \Phi\)，使得\((X_i, X_j) \in D_m\)时，就在这两个结点之间连上一条边，画上所有的这些边，就形成了Induced Markov Network。

有了分布P，又有个图H，那么就可以把BN的那套东西搞过来了。

首先是Factorizatioin的概念，当存在一个factor的集合\(\Phi\)，使用得\(P = P_{\Phi}\)并且H是\(\Phi\)的Induced graph时，就说P factorizes over H。实际上就是以\(\Phi\)作为中介，把P和H联系起来了。因为不同的\(\Phi\)可能会生成相同的H，所以H并不能完整表达P中的信息。

Flow of Influence：这个比BN要简单得多，没有什么v-structure这么变态的东西，只有在两个变量之间有一条active trail（即这条路径上没变量是被observed），那就这条influence就是通的。而且，两个变量间influence可能有多条活跃路径。最后，这种influence只依赖于这个graph，不依赖于factors。

Conditional Random Field

这东西跟前面的Gibbs Distribution很类似但是归一化方式不同，这也造就了它独特的地方和应用场景，当在做某些预测Y的任务而不想关心X_i之间的关联时还是很有用的。

假设有一组变量\(X_1,...,X_n\)，以及一个目标变量Y，我们想做就是找到从X到Y之间的条件分布\(P(Y|X)\)，以帮忙我们通过观测到一系列X来预测未知的Y。在图像实体识别中，X可以是图像中的元素值，Y可以是object label；在文本处理的例子中，X可以是句子中的各个word，而Y则是POS tag。

CRF具体形式与Gibbs分布几乎就是一样的，给定\(\Phi\)，然后利用factor product来得到unormalized measure，表示为\(\hat P\)。不同之处在于，后面归一化项（或者称为partition function）是不同的，如下

For Gibbs Distribution: \(Z = \sum_{X,Y} \hat P(X, Y)\)

For CRF: \(Z(X) = \sum_{Y} \hat P(X, Y)\)

前者归一化后得到的是联合概率分布\(P(X, Y)\)，而后者得到的则是条件概率分布\(P(Y|X)\)。

这个玩意儿有什么用处呢？假设所有factors的形式都是\(\phi(X_i, Y)\)，即没有任何的X变量之间的信息，如何我们使用这些factors来计算联合分布的话，实际上我们就做出了如朴素贝叶斯般的假设，即所有的X之间是独立的，显然这种假设在某些情况下是很粗暴的。而像前面提的这种通过X预测Y的场景下，X之间有啥关系我们是不关心的，我们只是想了解它们如何影响Y的取值，这种情况下利用CRF计算得到的条件概率分布就足够满足我们了，而不用去关心X之间会有什么联系。换个角度来说，前者计算出的联合分布实际是一个信息最全的分布，因为通过联合分布可以计算任意的条件分布和边缘分布，包括X之间的关联，但是有些信息我们实际是不关心的，也没有必要去model的；而条件概率分布虽然信息不如联合分布全（比如它就没有X之间关系的信息），但是对于我们的预测任务来说是足够的了。

课程中又提到CRF跟很多现有模型是有非常强的关联的，比如，Logistic Model就是CRF的一种特殊形式，很有意思，但是推导过程我就不写了，贴个图了事。

最后抄一句话做总结：CRF allows models with highly expressive features, without worrying about wrong independencies.

Independecies in Markov Networks

从这里开始会有一些很概念性的东西，虽然挺烦，但还是得写写。多数概念都是BN那边迁移过来的。

Seperation in MN: X and Y are separated in H given Z if there is no active trail in H between X and Y given Z.

I-Map：MN中的独立性集合表示为\(I(H) = {(X \perp Y| Z): sep_H(X, Y|Z)}\)，如果P满足这个\(I(H)\)，那么就说H是P的一个I-map。

Factorization => Indepedencies: If P factorizes over H, then H is an I-map of P. (If P factorizes over a graph H, we can read from the graph independencies that must hold in P (an independency map).)

Factorization <= Indepedencies: For a positive distribution P, if H is an I-map for P, then P factorizes over H.

我的一点理解是，H中的信息总是P的一个子集，P能够factorization不代表它所有的信息都能表达在H中。

I-maps and Perfect Maps

如果我们把一个概率分布P中所有的独立性约束都提取出来，表示为\(I(P)\)，那么对于P的任意一个I-map来说，都有\(I(G) \in I(P)\)，而反向则并不总是成立的。换句话说，G中的独立性约束总是P的一个子集，可能无法完整表达P中蕴含的信息。

当然，理想情况下，对于一个P，我们希望能得到一个能表达其完整的独立性信息的图G，因为这样的话，G中就包含了所有P中的独立性条件，图不但会更加informative，也会变得更加稀疏（因此也就会有更少的参数）。我们定义当满足\(I(G) = I(P)\)时，就称它为Perfect Map。

理想很丰满，但现实很骨感，对于一个P来说，想得到它的Perfect Map通常是很难的。举几个例子，

• 假设一个pairwise MN，而P是由它导出的一个包含其所有独立性信息的概率分布，我们希望得到一个BN的使其成为Perfect Map。事实证实，找不到这个样Perfect Map。
• 反过来，假设v-structure的BN，而P是由它导出的，我们希望能得一个包含Perfect Map的MN，事实证实，也是找不到的。
• 另外还有一个XOR的例子，我就不多说了。

前两个例子也说明，BN与MN之间的等价转换有时是不可行的，总是可能会丢失掉一些原有的信息。

更加让人崩溃的是，即使我们找到一个P对应的Perfect Map，也不能保证它是唯一的。比如，最简单BN模型，A->B, A<-B两个图的所表达的独立性信息就是相同的（实际都是空集）；再比如，三个变量的情况，除了v-structure中的X->Y<-Z之后，另外的三种图也是表达了相同的独立性信息。当两个图G,H中所包含的独立性信息相同，即\(I(G) = I(H)\)，那么就称二者是I-equivalent。多数图都有对应的很多I-equivalent变种。

Log-Linear Models

对于MN，除了使用factor product+normalize来表达联合概率分布外，还可以使用log-linear model来实现，表达式为

Factor Product: \(\hat P = \Pi_i \phi_i(D_i)\)

Log-linear Representation: \(\hat P = exp(-\sum_j w_j f_j(D_j)) = \Pi_j exp(-w_j f_j(D_j))\)

每个i表示factor的索引，每个\(D_i\)是相对于这个对应的factor来说的；相应地，每个j是feature的索引，所以\(w_j, D_j\)都是相对于这个feature的，也就是说每个feature会有一个对应的权重及它的scope。而不同的feature也可以有相同的scope。另外，需要注意一点，factor的scope和feature的scope甚至可以是不相关，因为feature和factor可以不存在一一对应的关系，从这个意义上讲，Log-linear Representation中的最后一个表达式中，每个\(exp(-w_j f_j(D_j))\)可以看作是重新定义的一个factor。

上面是两种不同的对联合分布的表示方法，所以需要首先证明Factor方式是可以等价地表达后Log-linear方式的。

假设有一个\(\phi(X_1, X_2), X_i \in {0, 1}\)，这个factor的取值分别为\(a_{00}, a_{01}, a_{10}, a_{11}\)，其中每个\(a_{ij} = \phi(X_1 = i, X_2 = j)\)。现在我们定义4个feature，分别为

\[f_1 = I\{X_1 = 0, X_2 = 0\}\]

\[f_2 = I\{X_1 = 0, X_2 = 1\}\]

\[f_3 = I\{X_1 = 1, X_2 = 0\}\]

\[f_4 = I\{X_1 = 1, X_2 = 1\}\]

其中I表示indicator function。于是，我们得到如下等式\(\phi(X_1, X_2) = exp(-\sum_k w_k f_k(X_1, X_2))\)，其中\(w_k\)为对应的\(a_{ij}\)的对数的相反数。这4个feature的scope是相等的，也对应了前面所说的“不同的feature也可以有相同的scope”。

后面就是一些应用的例子了。

首先是对于单词的注标问题，X表示当前的单词，Y表示这个单词的label。基于对这个领域的理解，我们可以定义如下的features

\[f_1(Y, X) = I\{Y = B\_PER, X~is~capitalized\}\]

\[f_2(Y, X) = I\{Y = B\_LOC, X~appears~in~atlas\}\]

......

然后就可使用这些features去构建一个log-linear model，表达对应的联合概率分布\(P(Y, X)\)。

第二个例子是Ising Model，没听懂具体是干什么用的，它的结构是pairwise MN，每个变量\(X_i \in {-1, +1}\)，定义两种features，一种是单变量的\(f_i(X_i) = u_i X_i\)，另一种是双变量的feature，即\(f_{i, j}(X_i, X_j) = X_i * X_j\)，其中\(f_{i, j}\)是说这个feature只会应用于\(X_i, X_j\)这两个变量上（scope），后面的内容会对它做扩展，这里先不管。对应的联合分布的表达式为

\[P(X) = exp(-\frac{1}{T} E(X))\]

\[E(X) = -\sum_{i<j} w_{ij} X_i X_j - \sum_i u_i X_i\]

最后一个例子是Metric MRF。一种被特别提到很常用feature称为metric，而它所对应的MN被称为metric MRF。在使用metric MRF的应用中，通常都希望相连的两个变量有相似的取值。

metric实际就是一个距离函数\(\mu : V * V \to R^{+}\)，其中V是每个变量\(X_i\)的取值空间。这个距离函数要求满足三个基本属性：自反性，对称性以及三角不等式条件。

\[f_{i, j}(X_i, X_j) = \mu (X_i, X_j)\]

\[P(X) = exp(-\sum_{i, j} w_{i, j} f_{i, j}(X_i, X_j))\]

这样就满足了当有边相联的两个变量取值不相似（即距离较远时），它会拉低这个assignment整体的联合概率。

一些常用的metric函数定义

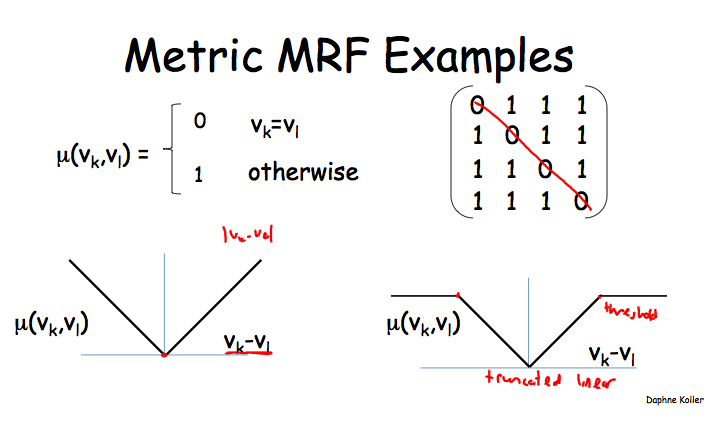
第一个定义就是说，只有当两个变量的取值相等时，距离为0，否则就为1；应用场景可以是image segmentation，它要求相邻的superpixel要共享同一个object label。

第二个定义就是取两个变量取值的差的绝对值，但是正如左下方的那图示意的一样，这个距离值可能是无界的，所以可以像右下角那样做一个truncate。对应的例子是图像除噪，假设有一幅有噪声的图像，其像素值表示为\(X_i\)，我们希望得到的是除噪后的图像，其像素表示为\(Y_i\)，约束条件是每个\(Y_i\)要与\(X_i\)接近，并且\(Y_i\)也要与它的邻像素值接近。如果采用未作truncate的metric函数，那么可能过于严苛，造成\(Y_i\)也要与它的邻像素值过于接近，而实际上这个局部特点并不是那么要严格遵守的，像物体边界上的像素值是有可能与其邻像素不一样的。这种应用场景下，truncate后的metric函数就更合适。

但是它相对于factor形式有什么优势呢？我的理解是，它可能更有利于adapt到某个特殊的领域，可以人工设计一些feature并很方便地将它们融入到模型中。

Shared Features in Log-Linear Models

回到刚才的Ising Model，当时就提了一下“\(f_{i, j}\)是说这个feature只会应用于\(X_i, X_j\)这两个变量上”，实际上这个feature可以不局限于仅仅是这两个特定的变量，可以是任何两个相邻的变量，同时这个feature对应的权重\(w_{ij}\)也是可以共享的。

\[-\sum_{i, j} w_{i, j} f_{i, j}(X_i, X_j) \to -\sum_{i, j} w f(X_i, X_j)\]

同样方式可以用到单词标注的问题上，对于任意的\(X_i, Y_i\)都可以定义通用的feature，而不必每一对变量都定义一个。Image Segmentation的例子也是如此。

因此，我们只需要为每个feature \(f_k\)定义一组scopes，表示为\(Scopes[f_k]\)，然后就有\(w_k \sum_{D_k in Scopee[f_k]} f_k(D_k)\)。

总之，相同的参数和结构模板可以同一个MN中复用（同一句话中不同的word及对应的label），同时也可以在不同的MN中复用（不同的句子中）。

(END OF THIS SECTION)