上一节提到的Conditional Probability Query和MAP中最关键的点就是要算贝叶斯公式中的分子，这个有了之后要么归一化要么取最大值，这事就搞定了。所以本节的这个VE算法就是用来算这个分子的。

Variable Elimination Algorithm

这个算法超级简单，就是每一步都尝试去掉其中的一个变量，方式是把所有与这个变量相关的factor都搞在一起，然后marginalize，生成的结果记作一个新的factor；然后选择另一个变量去重复上面的步骤，直至所有无关变量会都被eliminate掉了，这个事也就搞定了。直接给个例子，我们想算下面这个BN中P(J)的分布：

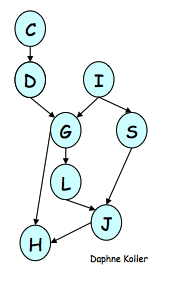
先把P(J)写成factor product的形式

\[\hat P(J) = \sum_{L,S,G,H,I,D,C} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_G(G, I, D) \phi_H(H, G, J) \phi_I(I) \phi_D(C, D) \phi_C(C)\]

假设我们按照C, D, I, H, G, S, L的顺序来依次做variable elmination，先来搞C，把所有跟C相关的factor放在一起，并把对C的求和push进去，形成

\[\hat P(J) = \sum_{L,S,G,H,I,D} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_G(G, I, D) \phi_H(H, G, J) \phi_I(I) \sum_C \phi_D(C, D) \phi_C(C)\]

重新定义一个新的factor，\(\tau_1(D) = \sum_C \phi_D(C, D) \phi_C(C)\)，代进去，得到

\[\hat P(J) = \sum_{L,S,G,H,I,D} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_G(G, I, D) \phi_H(H, G, J) \phi_I(I) \tau_1(D)\]

这样我们就成功把C去掉了，或者说marginalize C。下一步要去掉是D，同样的定义\(\tau_2(G, I) = \sum_D \phi_G(G, I, D)\tau_1(D)\)，代入上式中得到

\[\hat P(J) = \sum_{L,S,G,H,I} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I) \phi_H(H, G, J) \phi_I(I) \tau_2(G, I)\]

这样D也被干掉了。后面的工作以此类推，直到把等式右边非J的变量都干掉了，计算就结束了，我把最后一步写出来。

\[\hat P(J) = \sum_{L,S} \phi_J(J,L,S) \tau_5(L, J, S)\]

如果有Evidence咋办？凉拌！

\[\hat P(J, I=i, H=h) = \sum_{L,S,G,D,C} \phi_J(J,L,S) \phi_L(L, G) \phi_S(S, I=i) \phi_G(G, I=i, D) \phi_H(H=h, G, J) \phi_I(I=i) \phi_D(C, D) \phi_C(C)\]

就这么简单！

贝叶斯公式的分子算完了，如果想得到\(P(J|I=i, H=h)\)呢？正如前面所述，renormalize就可以了，归一化常量就是\(P(H=h, I=i)\)。

前面这个例子是BN，对MN其实也一样，都是对factor做处理，就不多费话了。

再来两张图，总结一下VE算法的关键步骤：

简单来说，把所有与变量Z相关的facor乘在一起，通过marginalize把Z干掉，得到的结果变成一个新的factor参与到下次的计算中；重复以上步骤即可。

Complexity Analysis

这部分是对VE算法的复杂度分析，比较无趣，但是跟后面的知识也有些关联，还是得写写。

VE算法执行的每一步由两部分组成：factor product + marginalization。先来看看每部分的有哪些工作量。

\[\psi_k(X_k) = \Pi_{i=1}^{m_k} \phi_i\]

这个是factor product的步骤，它把\(m_k\)个factor相乘。对于\(X_k\)的每一个assignment，需要每个factor都参与相乘，因此共有\(m_k - 1\)次乘法操作。而\(X_k\)有多少assignment呢？记这个数为\(N_k = |Val(X_k)|\)，于是这个factor product的步骤需要\((m_k-1)N_k\)次乘法。

\[\tau_k(X_k - \{Z\}) = \sum_Z \psi_k(X_k)\]

这个是marginalization的步骤，令\(N_k\)的定义不变，由于\(X_k\)的每一个assignment都要参与且仅一次参与marginalization求和的操作，因此这步需要花费掉\(N_k\)个加法操作。

ok，现在来看整个算法执行过程中的花费。假设有n个变量，m个factor（对于BN来说，m<=n，因为每个变量都有一个factor，如果算上evidence，那么有m<n的可能；而对于MN，通常有m > n，因为MN的factor可能是多个变量的组合，如pairwise factor）。在VE的每一次eliminate时，算法会生成一个新的factor，同时会eliminate至少一个变量。我们一共只有n个变量，所以至多会有n个eliminate的步骤，而总的factor数量\(m^* <= m + n\)，这里小于就是因为至多n次eliminate而生成新factor。

取VE执行过程中最大的factor的assignment数量为\(N = max(N_k)\)，于是

• Product operations: \(\sum_k (m_k-1)N_k <= N\sum_k(m_k-1)\)，而由于每个factor最多只参与一次factor product就被融入新生成factor之中了，所以上式至多为\(Nm^*\)；
• Sum operations: \(\sum_k N_k <= N*n\)，因为至多只有n次elimination操作。

这样看来，所有的花费相对于N, m, n都是线性的，但是N实际上相对于变量个数是指数级的，所以我们白高兴了。

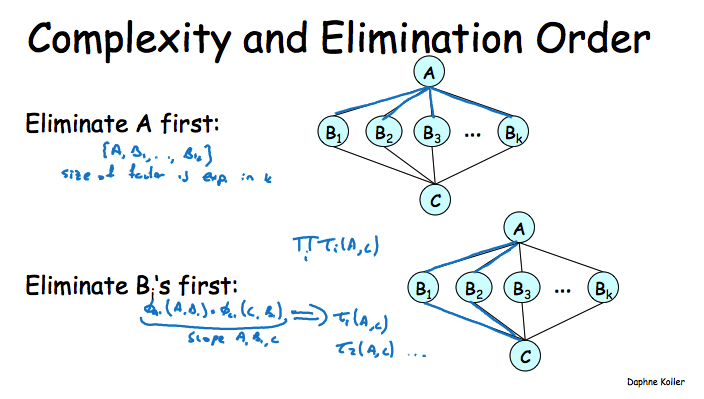
从上面这些分析来看，m和n不可变的情况下，我们要尽量不要在VE的执行过程中生成太大的factor，因为在变量的cardinality不可变的情况下，我们只能让factor不要包含太多的变量。而从一些例子中可以发现，Elimination Order对于控制N有着很大的作用，举一个比较极端的例子，下图中先去掉A时会生成一个包含k个变量的factor，而先去掉各个B时，生成factor只会包含2个变量。

Graph-Based Perspective

这一小节的内容核心是Induced Graph，先给出定义，然后再给例子。

定义于factors \(\Phi\)和elimination order  \(\alpha\)的Induced Graph \(I_{\Phi, \alpha}\)满足：1. 无向图；2. 如果两个变量\(X_i, X_j\)在按照\(\alpha\)来执行VE过程中出现在同一个factor中，而且原图上不存在边的话，那么它们之间就被连上一条filling edge。

换句话说，原图由于VE按照某种顺序执行过程而添加上一些边，这个生成的新图就是Induced Graph。原图是啥呢？就是由factors induce出来的MN，这个前面的章节里已经提过了。

下面给例子，先是原图，这个是通过BN->factors->MN来得到的。

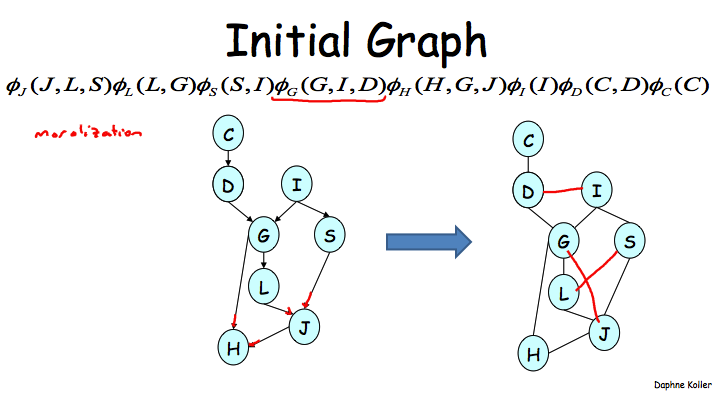
如果按照C, D, I的顺序来执行VE的话，那么干掉I之后就需要在G和S之间添加上一条边了，因为它们会同时出现在一个新的factor之中。

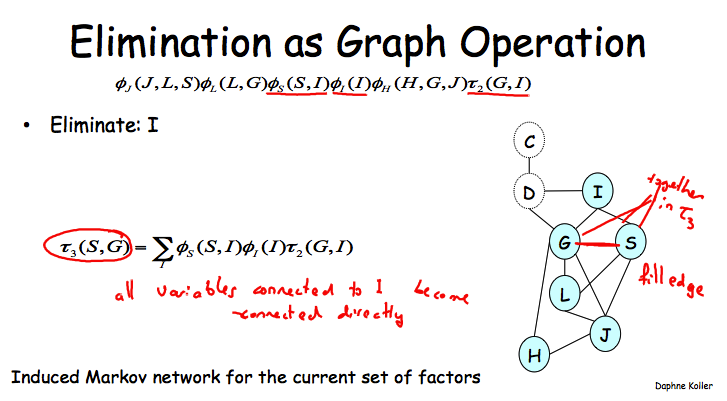
这个图跟VE的复杂性有啥关系吗？必须有！

Theorem: Every factor produced during VE is a clique in the induced graph.

clique就是一个maximal fully connected subgraph，也就是任意两个结点之间都一条边相连，而添加任意一个其实变量都不能使这个条件满足。结合clique的概念，其实上面这个定理很好理解，之所以生成一个新的factor是由于我们把与某个变量Z相连的所有factor都搞到一起了，而生成新的factor之后，Z的邻居们也肯定都有边相连（没有的都会被补上filling edge）。因为我们已经把Z的所有邻居都找来了，任意一个非Z邻居的变量都不可能加入这个clique，因为它至少无法与Z相连。

Theorem: Every clique in the induced graph is a factor produced during VE.

这个也很好理解，先给定出组成一个clique的K个变量，那么肯定会有一个变量在VE的过程中首先会被eliminate掉。因为在eliminate之后就不可能再有其它结点能与之相连了，所以此时它应该已经与clique中其它的K-1个变量都直接相连了。而在eliminate之后生成的新factor中，这K-1个变量必须都在其中，因此它们之间都会有边相连形成fully connected，所以此时这个clique就已经形成了。

然后就是Induced Width的概念：这个值就是Induced Graph中最大的clique的包含的结点个数-1。为啥减1呢？因为clique中实际是包含了被eliminate掉的那个变量，而生成的新factor则不包含这个变量，而前面一个小节也提到了VE的执行效率很大程度上受制于VE过程中最大的factor包含的变量个数（记作factor size），所以这样就有Induced Width = factor size。

因此最小化factor size等价于最小化induced width，于是就有了minimal induced width的概念：\(min_{\alpha}(width(I_{K, \alpha}))\)；它实际上就直接对应了一个VE算法执行效率的下界。

Finding Elimination Orderings

Theorem: 对于一个图H，判断是否存在一个elimination ordering使用得induced width <= k还是一个NP-complete问题。这日子没法过了！

另外注意的是，这个NP-hardness与inference问题的NP-hardness是独立的，也就是说，即使给出了一个最优的ordering，用它去做inference也同样是指数级的。

好吧，既然如此，我们只能求助于Greedy Search方法了，即每个步都优先干掉最小cost的那个变量，咋定义cost呢？

• min-neighbors: 当前图中的邻居数量
• min-weight: 新生成的factor的assignment数量
• min-fill: 最小数量的filling-edge，讲师说这个function效果好
• weighted min-fill: 新的filling edge的weight之和，每边edge的weight为其相联的两个node的weight的乘积。

Theorem: The induced graph is triangulated –  No loops of length > 3 without a “bridge”。这个定理不知道干啥用的，后面也没讲。。。

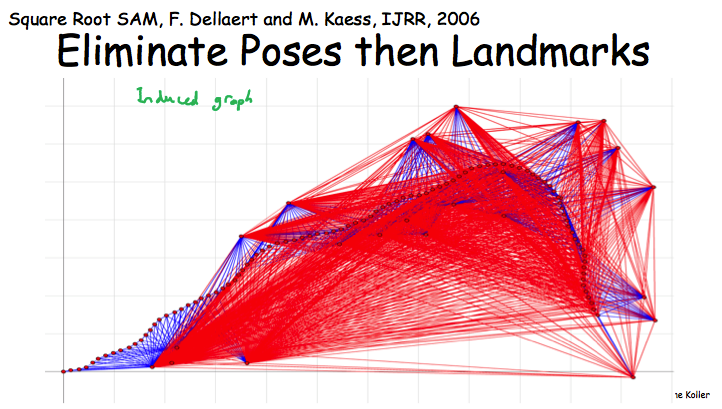
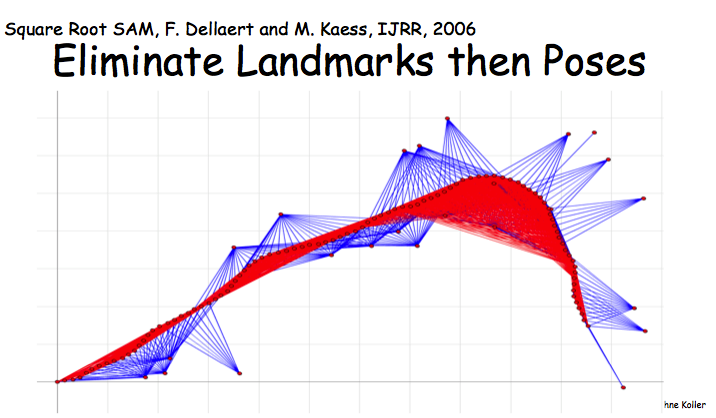
最后Robot Localization的例子，在这个MN中先eliminate landmards还是poses会形成两个密度差异很大的induced graph，而密度越大说明对应的factor包含的变量越大，VE执行起来也就越慢。