PRML Notes - 1.6 Information Theory
信息量和香农熵
一个变量取值的信息量可以看作是它带来的“使人惊讶的程度”,一个必然事件没有任何信息量,而一个极其偶然的事件的发生则会使人非常“惊讶”,因而包括大量信息。
自然地,信息量的概率就与变量的概率分布联系在了一起。香农熵(Shannon Entropy)成功表达了一个离散型变量所带来的平均信息量:
![\[ H(x)=-\sum_xp(x)log_2p(x)\] \[ H(x)=-\sum_xp(x)log_2p(x)\]](/user_files/ChillyRain/epics/de0e30ec0706b4933d9f0a0b56a26649d2736f19.png)
注意到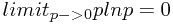 ,因此计算某个变量的香农熵时只考虑非零取值即可。另外,香农熵是非负的。
,因此计算某个变量的香农熵时只考虑非零取值即可。另外,香农熵是非负的。
无噪声编码定理:香农熵是传递一个变量状态所需要的比特数的下界。也就是说,在期望意义下,对一个变量的取值进行编码所需要的最小的比特数即为香农熵。一般情况下,香农熵对数的底取2。
对于一个概率分布,当概率集中于较少的某几个取值时(绝大多数情况下变量会取少数的几个值之一),香农熵的值会较低,相反地,如果概率在各种取值上比较平均(几乎无法判断变量会取哪个值),那么香农熵会较高。使用拉格朗日乘子法(约束概率分布的归一化)计算香农熵的最大值,可知当概率分布是均匀分布时,香农熵可取到最大值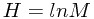 ,其中M为变量的状态总数(所有可能取值的个数)。因此,香农熵也可以看作是一个变量不确定度的度量。
,其中M为变量的状态总数(所有可能取值的个数)。因此,香农熵也可以看作是一个变量不确定度的度量。
物理上关于香农熵的解释:mulitplicity, microstate, macrostate, weight
连续型变量的微分熵
对于一个连续型变量,无法直接使用上面香农熵的定义。可以近似地对连续型变量的取值进行离散化,将整个取值范围划分成宽度为 的小区域。均值定值告诉我们,在每个小区域内总存在一个值
的小区域。均值定值告诉我们,在每个小区域内总存在一个值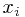 ,使得以下等式成立
,使得以下等式成立
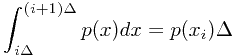
因此,我们可以把每个落入第i个小区域的的点赋予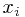 。这样,我们就可以套用离散型变量的香农熵公式
。这样,我们就可以套用离散型变量的香农熵公式
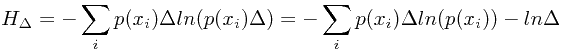
而当 趋近于0时,上式最右侧第二项趋近于0,而第一个项则趋近的表达式称为微分熵(differential entropy):
趋近于0时,上式最右侧第二项趋近于0,而第一个项则趋近的表达式称为微分熵(differential entropy):
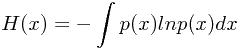
仍然使用拉格朗日乘子法,约束均值和方差,以及概率分布的归一化,可知在均值和方差一定的情况下,使微分熵最大的概率分布为正态分布。而正态分布的微分熵表达式为
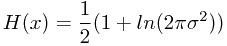
由以上的表达式可知,香农熵随着方差而增大。同时,我们也可以看出,与离散型变量的香农熵不同,微分熵可以是负的。
条件熵(conditional entropy)
![$$H[y|x]=-\int \int p(x,y)lnp(y|x)dydx$$ $$H[y|x]=-\int \int p(x,y)lnp(y|x)dydx$$](/user_files/ChillyRain/epics/3dc7a27c77ff5ee8d400c6d134419aa0b0ec893d.png)
![$$H[x,y]=H[y|x]+H[x]$$ $$H[x,y]=H[y|x]+H[x]$$](/user_files/ChillyRain/epics/02abd4c6cb6fa0a40b429a0ddf6892101596ac5d.png)
相对熵(relative entropy)
依然从编码角度来考虑,若一个变量的真实分布为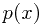 ,而我们实际上使用了
,而我们实际上使用了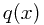 来对这个变量进行编码,那么由此而使用了的多余的比特数定义为相对熵或者KL距离(Kullback-Leibler divergence)。
来对这个变量进行编码,那么由此而使用了的多余的比特数定义为相对熵或者KL距离(Kullback-Leibler divergence)。
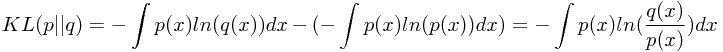
注意到,虽然名为距离,但是KL距离(相对熵)没有对称性。另外,相对熵是非负的,当且仅当 时相对熵取零。其证明用到了以下内容:
时相对熵取零。其证明用到了以下内容:
凸函数定义为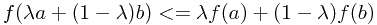 。等价地,函数的二阶导数各处均非负。如果仅当
。等价地,函数的二阶导数各处均非负。如果仅当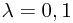 时等号成立,那个这个函数称为严格凸函数。凸函数的相反数为凹函数。香农熵为凹函数。
时等号成立,那个这个函数称为严格凸函数。凸函数的相反数为凹函数。香农熵为凹函数。
简森不等式(Jensen's inequality)
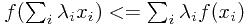 ,其中
,其中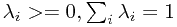 ,
, 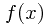 为凸函数
为凸函数
如果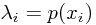 ,那么有
,那么有
-
连续型:
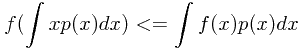
-
离散型:
![$$f(E[x])<=E[f(x)]$$ $$f(E[x])<=E[f(x)]$$](/user_files/ChillyRain/epics/079cd7d1d91437f86debf527fc4727c5299dd455.png)
于是,可证相对熵的非负性
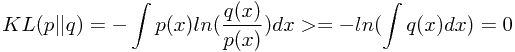
其中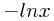 严格凸函数,因而当且仅当
严格凸函数,因而当且仅当 时取等号。
时取等号。
相对熵与似然函数的关系
假设未知真实分布为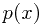 ,我们希望使用一个参数模型
,我们希望使用一个参数模型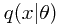 结合N个观测数据来确定一个最优的
结合N个观测数据来确定一个最优的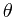 来模拟真实分布。一种自然的方法是使用KL距离做为误差函数,以最小化
来模拟真实分布。一种自然的方法是使用KL距离做为误差函数,以最小化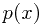 和
和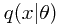 的KL距离为标准来确定最优的参数值。
的KL距离为标准来确定最优的参数值。
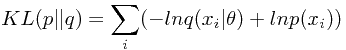
将上面的误差函数相对于参数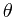 求导,可知:最小化KL距离等价于最大化似然函数。
求导,可知:最小化KL距离等价于最大化似然函数。
互信息(mutual information)
互信息描述了两个变量之间互相包含关于对方的信息量。定义为两个分布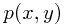 和
和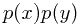 之间的KL距离
之间的KL距离
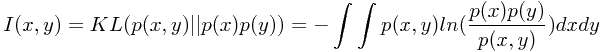
根据相对熵的非负性可知,互信息是非负的,当仅且当两个变量相互独立时互信息为零。
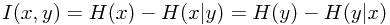
由此可知,互信息可以看作,当已知一个变量的情况下,另一个变量不确定性降低的程度。
[终于搞定了第一章,春节假期任务完成^_^]