PRML Notes - 1.5 Decision Theory
概率论为我们提供了一个用于表达不确性的框架,而最终我们需要使用这个框架所提供的内容来做出决策,比如,预测某个文本的真正的类别是什么。这就是决策论所扮演的角色。
推演和决策
推演(inference)指通过给定的有限的数据集,学习得到输入变量x与响应变量t的联合概率分布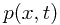 ;
;
决策(decision)指根据我们对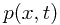 的理解,如何在面对新的问题时(x)去做出最优的决定(t)。
的理解,如何在面对新的问题时(x)去做出最优的决定(t)。
在分类问题中,我们需要决策的就是面对新的样本点,应该它哪一个类标签。而这个问题在贝叶斯框架下,很自然地我们对给定一个样本后,其属于各个类的后验概率更感兴趣。
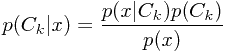
如果我们的目标是最小化将样本分错类的可能性,那么直觉上这就变成了计算MAP的问题。
最小化错分比率
假设我们将输入空间X分成不同的决策区域(decision regions),每个决策区域记为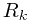 。每个区域记录了算法每个样本的决策类别,而区域之间的边界即为决策边界或者决策面。以二分类问题为例,一个样本被错分的可能性可表示为
。每个区域记录了算法每个样本的决策类别,而区域之间的边界即为决策边界或者决策面。以二分类问题为例,一个样本被错分的可能性可表示为
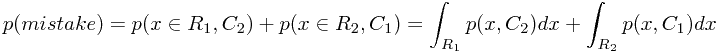
其中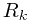 表示决策类别,
表示决策类别,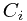 表示真实类别。很自然地,如果对于一个输入x,
表示真实类别。很自然地,如果对于一个输入x, ,那么就应该将该样本分到第一个类的决策区域
,那么就应该将该样本分到第一个类的决策区域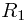 之中,以最小化上面这个误差函数。而通过乘法法则可知
之中,以最小化上面这个误差函数。而通过乘法法则可知
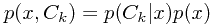
因此,对于每个样本,我们都应该将其赋予其MAP所对应的类。对于多分类问题,通过最大化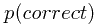 会更方便一些,但是结论是相同的:计算每个样本的MAP。
会更方便一些,但是结论是相同的:计算每个样本的MAP。
最小化期望损失
更实际一些,不同类别判错的代价也是不相同的。例如,将某种疾病阴性的人判为阳性的代价(一些不安,以及进一步检查的费用),就明显小于,将阳性的人判为阴性(可能会错过治疗的最佳时机而死亡)。为了反映这种情况,损失函数(loss function)的概念被提出来。更进一步地,我们引入了损失矩阵(loss matrix),其中每个元素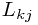 表示当某样本真实类别为k,而被决策为j时带来的损失。
表示当某样本真实类别为k,而被决策为j时带来的损失。
理想情况下,我们希望获得使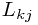 最小的j,而实际上我们却无从了解真实类别k的值。因此,实际使用的方法涉及了推演步骤中得到的联合概率分布
最小的j,而实际上我们却无从了解真实类别k的值。因此,实际使用的方法涉及了推演步骤中得到的联合概率分布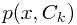 ,使这个信息来计算平均损失,并以最小化平均损失为目的来做出决策:
,使这个信息来计算平均损失,并以最小化平均损失为目的来做出决策:
![$$E[L]=\sum_{k}\sum_{j}\int_{R_j}L_{kj}p(x, C_k)dx$$ $$E[L]=\sum_{k}\sum_{j}\int_{R_j}L_{kj}p(x, C_k)dx$$](/user_files/ChillyRain/epics/5b8f04f61e2606170dce0deaa7b35c6d453ea2f1.png)
而对于上式中的每个样本x,我们需要做的是最小化
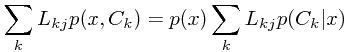
因此,对每个样本决策步骤中,我们需要做的就是最小化上式右侧的第二项(除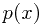 之外的部分)。
之外的部分)。
拒绝决策选项
当对于一个样本x,如果其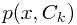 对于所有的k都有着相似的概率,那么,算法对这个样本的决策将不那么肯定。对于这种情况,最好是让机器放弃决策,而是提示让人工来确定。为此,需要设定一个阈值
对于所有的k都有着相似的概率,那么,算法对这个样本的决策将不那么肯定。对于这种情况,最好是让机器放弃决策,而是提示让人工来确定。为此,需要设定一个阈值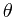 ,如果最大的后验概率
,如果最大的后验概率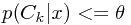 ,那么机器就拒绝做出决策。注意到,当阈值取1时,所有样本将被拒绝,而如果取1/K时,没有样本将被拒绝。
,那么机器就拒绝做出决策。注意到,当阈值取1时,所有样本将被拒绝,而如果取1/K时,没有样本将被拒绝。
学习过程的种类
至今我们把学习过程划分成了推演和决策两个步骤,实际上,解决问题的方式可以有以下三种
-
生成模型(generative model):显式或稳式地(可能是分别计算出似然性和先验)计算出联合概率分布
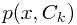 ,然后计算出后验概率分布,再进行决策。
,然后计算出后验概率分布,再进行决策。 - 区分模型(discrimitive model):直接计算后验概率分布,不必完全了解联合分布,然后进行决策。
- 区分函数(discrimitive function):直接学习到一个函数,将输入直接通过这个函数映射到一个类标签,它将推演和决策合为一体。
生成模型计算消耗较大,但是通过联合分布可以了解得到一些额外的信息,比如可以通过归一化得到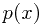 ,从而了解一个待测样本点是噪声点的可能性有多大(噪声检测)。区分函数的方法最直接,绕过了后验分布的计算,但是在一些情况下,后验分布还是很有意义的,可以简化一些计算过程。
,从而了解一个待测样本点是噪声点的可能性有多大(噪声检测)。区分函数的方法最直接,绕过了后验分布的计算,但是在一些情况下,后验分布还是很有意义的,可以简化一些计算过程。
-
最小化期望损失:如果损失矩阵是经常变动的,那么如果已有后验概率分布,那么可以直接使用它来计算新的损失矩阵下各样本的分类(根据
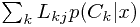 ),否则可能就需要将算法重新跑一遍。
),否则可能就需要将算法重新跑一遍。 - 拒绝决策选项:必须需要后验分布才成奏效。
- 补偿先验:为了模型学习的有效性,我们需要人工构造出各类内训练数据量相等的数据集,在计算出后验分布后,再通过乘除运算将模型中的人工先验替换成实际中的真实先验。
- 合并模型:如果输入变量的两个特征子集之间是独立的,那么可以分别计算每个特征子集的后验概率分布,再使用一些方法合并两个分布。例如,朴素贝叶斯模型。
回归损失函数
面向连续型变量的学习过程称为回归。此时推演的过程仍然是计算得到x与t的联合概率分布,而决策的过程就是得到输入变量x的响应估计值y(x)。与分类问题的决策过程相似,回归问题也需要一个损失函数,而一个常用的损失函数称为平方误差(square loss)。相应的,期望平方误差为
![$$E[L]=\int\int(y(x)-t)^2p(x,t)dxdt$$ $$E[L]=\int\int(y(x)-t)^2p(x,t)dxdt$$](/user_files/ChillyRain/epics/6fb8e159ddd66f77739390ec5d279c5ef3a32904.png)
我们的目标就是选择一个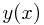 以最小化
以最小化![$E[L]$ $E[L]$](/user_files/ChillyRain/epics/8c86313fc463939b892b15677b4a2cb00a929b1f.png) 。通过计算损失函数
。通过计算损失函数![$E[L]$ $E[L]$](/user_files/ChillyRain/epics/8c86313fc463939b892b15677b4a2cb00a929b1f.png) 相对于
相对于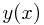 的导数,可得
的导数,可得
![$$y(x)=E_t[t|x]=\int tp(t|x)dt$$ $$y(x)=E_t[t|x]=\int tp(t|x)dt$$](/user_files/ChillyRain/epics/16dd5827a3a2ac7226a6e5a57c58d439e04cc629.png)
即给定x后的响应t的条件平均值,这个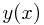 也称为回归函数(regression function)。从另一个角度来看,
也称为回归函数(regression function)。从另一个角度来看,
![$$(y(x)-t)^2=(y(x)-E[t|x]+E[t|x]-t)^2$$ $$(y(x)-t)^2=(y(x)-E[t|x]+E[t|x]-t)^2$$](/user_files/ChillyRain/epics/f7342b17b7fbba967f42e23e7b8c5acda598f289.png)
代入![$E[L]$ $E[L]$](/user_files/ChillyRain/epics/8c86313fc463939b892b15677b4a2cb00a929b1f.png) 可得如下形式
可得如下形式
![$$E[L]=\int(y(x)-E[t|x])^2p(x)dx + \int(E[t|x]-t)^2p(x,t)dxdt=bias+variance$$ $$E[L]=\int(y(x)-E[t|x])^2p(x)dx + \int(E[t|x]-t)^2p(x,t)dxdt=bias+variance$$](/user_files/ChillyRain/epics/f31309702d8e578561768115631a7c0b1aa3722d.png)
为最小化上面这个损失函数,等式右侧第一项当![$y(x)=E_t[t|x]$ $y(x)=E_t[t|x]$](/user_files/ChillyRain/epics/fab8289de3ac90d7d25ff3b46570fe1b85e24741.png) 时取得最小值为零,而第二项则表示了期望意义下输入变量x的响应值t的波动情况(方差)。因为它仅与联合概率分布有关与
时取得最小值为零,而第二项则表示了期望意义下输入变量x的响应值t的波动情况(方差)。因为它仅与联合概率分布有关与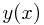 无关,所以它表示了损失函数中无法约减的部分。
无关,所以它表示了损失函数中无法约减的部分。
与分类问题相似,回归问题学习的过程可以分为
-
学习得到联合分布,再归一化得到条件分布,最后得出条件均值
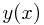 ;
; -
直接得到条件分布,再计算条件均值
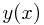 ;
; -
直接从训练数据中获得
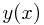 。
。
当然,平方误差并不是唯一可能的误差函数。平方误差的一般化称为明科夫斯基误差(Minkowski loss),其相应的期望误差为
![$$E[L_q]=\int\int|y(x)-t|^qp(x,t)dxdt$$ $$E[L_q]=\int\int|y(x)-t|^qp(x,t)dxdt$$](/user_files/ChillyRain/epics/baad69b4ed989e77e0136965df8d6ccbd08e8d3f.png)