PRML Notes - 1.2 Probability Theory
模式识别过程中使用的数据集的特点确定了整个学习过程中具有不确定性。一方面,数据集中的样本容量是有限的,无法完整刻画数据中的规律;另一方面,现实世界中的数据集几乎总是有噪声的。
基本概念
加法规则,乘法规则,边缘分布,联合分布,条件概率,贝叶期定理(先验概率,后验概率),条件独立。
对于一个连续型变量,当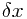 趋近于0时,
趋近于0时,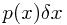 的取值称为该变量在此处的概率密度(probability density),
的取值称为该变量在此处的概率密度(probability density),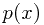 称为该变量的概率密度函数。概率密度满足非负性和归一化性质。对于一个离散型变量,
称为该变量的概率密度函数。概率密度满足非负性和归一化性质。对于一个离散型变量,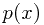 称为该变量的概率质量函数(probability mass function)。
称为该变量的概率质量函数(probability mass function)。
当两个连续型变量存在非线性关系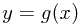 ,那么需要保证
,那么需要保证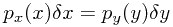 ,从而得到两个概率密度函数的关系
,从而得到两个概率密度函数的关系
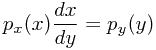
基本统计量
期望,条件期望,方差,方差与期望的等式关系,协方差
概率的定义
- 频率角度:N(N趋近于无穷)次实验中,某件事情发生的次数M与N的比值。
- 贝叶斯角度:不确定性的度量(或者置信程度的度量)
例如,多项式拟合的示例中,带有噪声的响应变量,其取值可以使用频率角度来解释,而对于学习得到的模型参数的不确定性,则需要使用贝叶斯角度来解释。
贝叶斯概率
假设D为数据集,w为模型参数。通过贝叶斯定理,
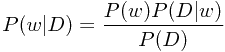
可以发现对比先验分布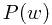 和后验分布
和后验分布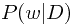 ,我们对模型参数取值的置信度发生了变化,而触发这种变化的正是我们所观察到的数据,更准确地说是基于先验分布而得到的数据的似然性
,我们对模型参数取值的置信度发生了变化,而触发这种变化的正是我们所观察到的数据,更准确地说是基于先验分布而得到的数据的似然性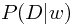 。在给定参数值的情况下,似然性越大,说明这个取值与观察数据更加符合,我们也会在后验中更加确信(注意到似然性与后验是正比的关系),否则确信度就会降低。
。在给定参数值的情况下,似然性越大,说明这个取值与观察数据更加符合,我们也会在后验中更加确信(注意到似然性与后验是正比的关系),否则确信度就会降低。
后验概率 正比于 先验概率*数据似然性
似然性函数(likelihood function)在频率观点和贝叶斯观点中都极其重要,但是在两种不同框架下的用法是截然不同的。
- 在频率观点下,参数值被认为是一个定点,是根据观测数据结合某个方法得到的。参数估计值的偏差或不确定性是通过取所有可能的数据集计算得到的一系列参数值的方差来评估的。
- 在贝叶斯观点下,参数的取值被认为是不确定的,而数据集是唯一的,因此输出的是一个关于这个参数的分布,并以此来表示参数取值的不确定性。
频率框架下的一种常用的估计方法为极大似然估计法(ML estimator)。目标的误差函数被定义为“似然性的负对数”,并此为目标来估计出能使此误差函数最小的参数值。正如前面所说,此方法针对一个数据集,只有能得一个定点的参数估计值,要评估其波动性,需要使用多个数据集分别进行参数估计,再统计这些估计值的方差等指标。一种可行的方法是使用重采样技术,如bootstrap,来从原始数据集中衍生出多个数据集,再对参数的波动性。
在贝叶斯框架下,算法的输出自然地是一个关于参数的概率分布,从而表达了这个参数的不确定性。贝叶斯框架的一个重要优势在于其可以融入一些先验知识,从而使结果不容易出现过拟合。然而,先验也同时是贝叶斯框架遭人诟病之处,因为它具有主观色彩。有些时候人们对先验的选择仅仅是根据其是否便于数学推导而进行,但是先验选择是否合适对最终的效果影响很大。非信息性先验(Noninformative Prior)可以缓解对先验主观性的依赖,但是却无法保证其是否合适,是否能达到良好的效果。同时,在做模型选择时,不同的先验也使比较无法平等进行,这时就不得不使用频率框架下的交叉验证等模型选择方法。
正态分布
正态分布也称为高斯分布,是一种常见的连续型概率分布。其单元变量的概率密度函数形式为
![]()
其中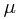 为期望,
为期望, 为方差。方差的倒数称为精度,记作
为方差。方差的倒数称为精度,记作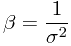 。一个概率分布的最大值称为它的mode,正态分布的mode位于其期望处。
。一个概率分布的最大值称为它的mode,正态分布的mode位于其期望处。
对于N个独立同分布(iid)的样本,其在正态分布下的对数似然性为
![]()
使以上对数似然函数最大的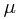 和
和 ,称为正态分布期望和方差的极大似然估计值。特别地,二者的求解是相互解耦的,即求解
,称为正态分布期望和方差的极大似然估计值。特别地,二者的求解是相互解耦的,即求解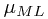 的过程是可以独立于
的过程是可以独立于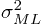 的求解过程的。
的求解过程的。
![]()
![]()
一般地,极大似然估计方法是容易过拟合的。特别地,以上对方差的估计值是有偏的(bias):
![]()
因此,可以相应地对方差的极大似然估计值乘以N/(N-1)的系数,来使其变成无偏估计。同时我们也注意到,若使样本容量N趋近于无穷,那么极大似然估计出的方差值也是会趋近于真实的方差值的。然而样本容量终究是有限的,特别地,当模型复杂度很高时,过拟合所引起的bias问题就会显得犹为严重。
正态分布可应用于多项式拟合问题,一般情况下,可以假设在某个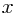 处的响应值
处的响应值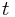 是符合以下分布的
是符合以下分布的
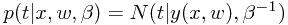
或者说,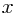 处的响应值会受到分布为
处的响应值会受到分布为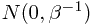 的噪声的影响。
的噪声的影响。
在给定了训练数据集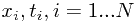 之后,我们可以使用前面的极大似然估计法来计算出分布的
之后,我们可以使用前面的极大似然估计法来计算出分布的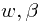 值,从而得到每个
值,从而得到每个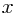 处其响应值的概率分布。
处其响应值的概率分布。
![]()
对以上对数似然性函数求w的导数,可以发现,其等价于最小化Sum-of-squares误差函数所得到的结果。由此可知,正态噪声分布的假设下,最大化似然函数值等价于最小化Sum-of-squares误差函数值。
同样地,可以在计算求得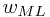 后独立地计算
后独立地计算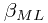 (同样是求导的方法)。在二者都确定之后,就得到了一个预测分布(predicitive distribution)。
(同样是求导的方法)。在二者都确定之后,就得到了一个预测分布(predicitive distribution)。
更进一步地,我们不止最大化似然函数,可以为参数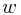 引入一个先验分布,来反映在未观察到任何数据之前,对这个参数取值的偏好。简单起见,可以假设这个也是如下形式的正态分布,
引入一个先验分布,来反映在未观察到任何数据之前,对这个参数取值的偏好。简单起见,可以假设这个也是如下形式的正态分布,
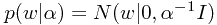
其中的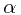 控制了模型参数
控制了模型参数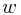 的取值,因此被称为超参数(hyperparameter)。根据后验分布正比于似然性函数乘以先验分布的关系,可得后验分布的形式为
的取值,因此被称为超参数(hyperparameter)。根据后验分布正比于似然性函数乘以先验分布的关系,可得后验分布的形式为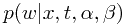 。接下来可以通过最大化这个后验分布函数来取得最可能
。接下来可以通过最大化这个后验分布函数来取得最可能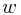 值(maximum posterior, MAP)。而在此求解过程中也会发现,最大化后验分布函数等价于规则化参数
值(maximum posterior, MAP)。而在此求解过程中也会发现,最大化后验分布函数等价于规则化参数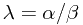 的岭回归。
的岭回归。
以上的两种方式终究仍然是对参数的点估计。采用更贝叶斯一点的方法,我们需要得到的是参数的概率分布,并通过积分来结合参数所有的可能值来做出决策。
假设参数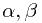 是已知的,那么预测分布可以表示为
是已知的,那么预测分布可以表示为
![]()
其中被积函数的第二项即为w的后验分布,这个等式表示为了得到x的预测响应值,应该根据每个w的后验概率来计算每个对应的响应估计值的加权平均。后面的章节会提到,实际上这个后验分布也是正态分布,因此整个预测分布也是正态分布,而其方差为
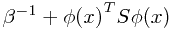
其中第一项反映了由于噪声而引起的响应值t的波动,而后一项则反映了参数w的波动(后验概率分布,非点估计)。