PRML Notes - 1.1 Introduction
模式识别的目标
自动从数据中发现潜在规律，以利用这些规律做后续操作，如数据分类等。
模型选择和参数调节
类似的一族规律通常可以以一种模型的形式为表达，选择合适模型的过程称为模型选择（Model Selection）。模型选择的目的只是选择模型的形式，而模型的参数是未定的。
从数据中获得具体规律的过程称为训练或学习，训练的过程就是根据数据来对选定的模型进行参数调节（Parameter Estimation）的过程，此过程中使用的数据为训练数据集（Training Set）。
对于相同数据源的数据来讲，规律应该是一般的（泛化Generalization），因此评估一个学习结果的有效性可以通过使用测试数据集（Testing Set）来进行的。
预处理
对于大多数现实中的数据集来讲，使用其进行学习之前，通常需要进行预处理，以提高学习精度及降低学习的开销。
以图像识别为例，若以像素做为一个特征，往往一幅图像的特征就能达到几万的数量级，而很多特征（如背景色）都是对于图像辨识起不到太大作用的，因此对于图像数据集，预处理过程通常包括维数约减（特征变换，特征选择），仅保留具有区分度的特征。
文本数据分类任务中，对训练文本也有类似的处理方式，只不过此时扮演特征的是单词，而不是像素值。
监督学习和非监督学习
输入向量（input vector）：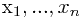
，响应向量（target vector）：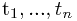
监督学习采用的数据集是包括输入向量和目标向量的，其目标就是发现二者之间的关系，学习的结果表示为函数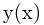
，使用函数的输出来近似响应值。如果
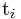为离散值，则此类学习任务称为分类（classification），若为连续值则称为回归（regresssion）。
非监督学习使用的数据集只包括输入向量，目的是直接探索数据的内在结构。发现数据中相似的簇的任务称为聚类（clustering），计算数据分布情况的任务称为密度估计（density estimation），将数据映射到三维及以下的任务称为可视化（visulization）。
还有一种学习形式，称为加强学习（reinforcement learning），指在一定的环境下，发现最合适的决策来最大化收益。通常这类学习任务需要在使用（exploit）和探索（explore）之间做出权衡。
Example：多项式回归
给定了数据集（输入向量和响应向量），首先进行模型选择，选定多项式的阶数。高阶的多项式模型是包含低阶多项式模型的（可将高阶项的系数设为零，从而退化成低阶模型），因此高阶模型拥有比低阶模型更强的拟合数据的能力。使用相对于数据来讲过强的模型，会使模型不但捕获数据中的规律，而会拟合进噪声，造成泛化能力不佳，这种情况称为过拟合（overfitting）。相反地，如果使用了相对于数据来讲太弱的模型，就无法捕获数据中的规律，这种情况称为欠拟合（underfitting）。选择合适的模型阶数是学习成功的前提条件，模型选择的方法包括基于经验的bootstrap，cross-validation以及基于信息论的AIC，BIC，MDL等。
在选好模型阶数，确定模型之后，下一步的工作就是参数调节（或称参数估计）。成熟的模型一般都有其相应的参数估计方法，如GMM-EM，RBF-BP，AR-YW等。对于多项式模型可采取较为一般的方法，即定义一个误差函数，通过求导数来计算得到误差最小值时的参数值。
Sum-of-square误差函数：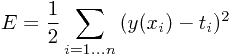
Root-mean-squre误差函数：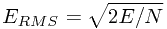
（单样本误差）
当过拟合发生时，训练得到多项式曲线表现得波动极大，相应地模型参数的模也很大。当数据量足够大时，模型发现过拟合的概率降低，因为模型总是在参数估计中尽可能地去迎合数据，从这个角度讲，数据越多，对模型的约束就越大。
如果希望使用一个相对复杂的模型，而不产生过似合现象，一种可行的方法是在误差函数中加入规则化项（regularization term），以约束模型系数的模。使用2-范数来做规则化项，得到修改后的Sum-of-square误差函数表示为
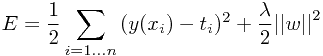
使用此误差函数进行学习的过程也称为岭回归（ridge-regression）或者权重退化（weight decay）。本质上，规则化项的引入是把一个参数转化为了另一个参数，即将模型阶数M转化成了系数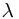
，并没有使学习过程变成更有效，
