PRML Notes - 1.4 The Curse of Dimensionality

前面的内容基本上都是基于单元变量的，而实际的绝大部分情况下，我们需要面对的是多元变量，这时候数据的稀疏性就会展现出来，导致一些看似科学而优雅的算法根本无可适从。这种现象就被称为维数灾难。

Examples：多数投票和多项式模型

多数投票是一种简化的KNN分类方法。假设我们有一些已分类的数据点，同时数据是平滑的，我们可以先挑出与待分类点最近的K个点，并根据这K个点的类标签来统计出哪个类在这个局部内是最可能出现的，并将此类标签赋予待测分类点。在低维数据集中，这个方法是简单而有效的，然而，当维数增大，这种方法很快就失效了，因为所需要的数据量会随着维数而呈指数级别的增长。

多项式模型的复杂度也会随着维数的增长而变大，导致模型的不可用。例如，3阶多项式模型，对于D维变量的多项式形式为

$$y(x, w) = w_0 + \sum_{i=1}^{D}w_ix_i + \sum_{i=1}^{D} \sum_{j=1}^{D}w_{ij}x_ix_j + \sum_{i=1}^{D} \sum_{j=1}^{D} \sum_{k=1}^{D}w_{ijk}x_ix_jx_k$$

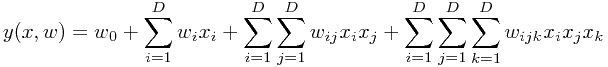
独立参数的个数变为了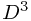$D^3$，更一般地，对于M阶模型，这个数字将变为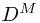$D^M$。虽然这个数字只是随着D而呈幂律增长，但是也足以让这个模型的参数估计由于数据量的不足而变得极度困难，最终致使模型无法使用。

几何直觉

我们考虑D维空间中的球体。首先，半径为r的D维球体的体积为

$V_D(r)=K_Dr^D$

接下来，考虑半径为r=1的D维单位球体的体积，与半径为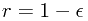$r=1-\epsilon$的球体体积之间的一层球壳，与单位球体体积的比例为

$$\frac{V_D(1)-V_D(1-\epsilon)}{V_D(1)}=1-(1-\epsilon)^D$$

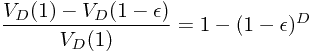
当维度D趋近于无穷时，这个比例趋近于1，也就是说当维数足够大时，几乎所有的体积都聚集中一个球体表面的薄壳之中。相似地，分析极坐标下的多元正态分布，当维数趋近于无穷时，绝大多数概率都集中在以r为半径的很薄的壳中。

这意味着低维空间下的机器学习算法，有可能在高维空间中变得完全不可用。然而，应用于高维空间的方法也是存在的。首先，数据很可能只存在于高维空间上的一个低维流形(manifold)上，通过流形学习(manifold learning, e.g. Isomap, LLE)算法可以有效地降维。其次，实际数据中往往存在局部平滑性（smothness），因此可以采用局部类插值技术去对未知数据进行预测。

Posted by Chilly_Rain 2012年1月25日 18:02

Category: Pattern Recognition and Maching Learning Tag: 维数灾难 Comment: (4)